This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
Peter Scholze, one of the four Fields Medalists recognized at the International Congress of Mathematicians at the beginning of August, studies algebraic geometry. One of the motivating questions in that field is when there are whole number or rational number solutions to polynomial equations. For example, the equation x^2+y^2+z^2=1, which defines a sphere in three-dimensional space, has the point (3/13,4/13, 12/13) as a solution.
In his Fields Medal lecture, Scholze talked about his work in p-adic geometry. (You can read a survey article he wrote to accompany the lecture here, though frankly if you can read that, you don’t need to be reading my post about it because you’re well ahead of me in your understanding of the p-adics.) The p-adics are an alternative number system, sometimes more useful than the real numbers for tackling problems in algebraic geometry and number theory.
There are several roads that lead to the p-adics. One way to get there is to start with absolute values. We’re used to the standard absolute value, which measures a number’s distance from 0. If a number is greater than 0, its absolute value is just itself, and if a number is less than 0, its absolute value is the opposite of itself. So |1|=1 and |-1|=1.
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
We can introduce a different way of measuring a number’s size, though, based on its relationship to a number p. If you’ve taken some advanced math classes, p is probably making your spidey sense tingle. Mathematicians usually use the letter p when they’re talking about prime numbers, and for the rest of the post, we’ll just assume p is prime. When talking about the p-adics for a specific p, mathematicians replace p with the number itself, so we talk about 2-adics, 3-adics, 29-adics, 314159-adics, you get the idea. (Yeah, 314159 is prime. Even my Pi Day curmudgeon heart flutters a little at that.)
A number’s p-adic absolute value is the reciprocal of the largest power of p that divides it. This is a case where a specific example can make that complicated idea a little easier to parse. Let’s look at the 3-adics first. The number 4 isn’t divisible by any positive power of 3. It’s equal to 30x4. That means 1 is the largest power of p that divides 4, making the p-adic absolute value of 4 equal to 1/1, or 1. The number 6 is a little more interesting. It’s equal to 31x2, making its absolute value equal to 1/3. The 3-adic absolute value of 54 is 1/27 because 27 is the largest power of 3 that divides 54. Multiples of very large powers of 3 have very small p-adic absolute values.
3Blue1Brown also explains the idea of p-adic numbers, using the example of 2-adics, in this video.
The p-adic absolute value has some interesting properties the normal one doesn’t. For example, there are a lot of numbers that share an absolute value. The numbers 1, 2, 4, 5, 7, 8, and an infinite string of other numbers all have 3-adic absolute value 1. The numbers 3, 6, 12, 15, 21, 24, and so on all have absolute value 1/3. Our usual absolute value only allows us to have at most two numbers with the same absolute value. Additionally, rather than numbers being able to have a continuous range of absolute values, they have a discrete set of options. There are an infinite number of them, but any number’s size must be a power of p. So there’s no number with 3-adic absolute value of 1/2 or 7. We’re thinking about numbers in a strange and different way.
The p-adic absolute value gives us a new way to measure the distance between two numbers. The p-adic distance between two numbers x and y is the p-adic absolute value of the number x-y. So going back to the 3-adics, that means numbers are closer to each other if they differ by a large power of 3. The numbers 1 and 4 have a difference of 3, so their 3-adic distance from each other is 1/3. But the numbers 1 and 19 have a 3-adic distance of 1/9 (18=32x2), and 1 and 82 have a 3-adic distance of 1/81. The numbers 11 and 29 have a difference of 18, so they have a 3-adic distance of 1/9.
If you’ve worked with modular arithmetic, this might be feeling sort of familiar. In arithmetic modulo, or mod, the number n, you only care about how close a number is to a multiple of n. The numbers 2, 9, and 93 are equivalent mod 7 because they’re all 2 more than a multiple of 7. In some ways, the p-adic distance sort of feels like you care about numbers mod pk for all powers pk at once.
One way to try to understand a new way of measuring distance is to try to figure out what is close to what in this distance. In the 3-adic metric, positive whole numbers are a maximum of 1 unit away from each other, so we can think about all of them as living in this bounded circle.
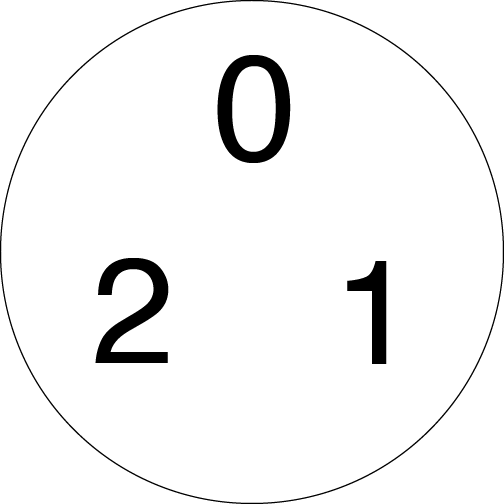
The numbers 0, 1, and 2 sitting in a 3-adic bubble. All other positive whole numbers also sit in this circle, but we can see a structure emerge in a neat way if we just start with these numbers. Credit: Evelyn Lamb
Let’s think of this circle as meaning anything within the circle is distance at most 1 away from anything else. Right now I just have the numbers 1, 2, and 3 in there, but all whole numbers 0 and larger are in there because they’re all at most distance 1 away from each other.
Now we can add another layer. The number 3 is only 1/3 away from the number 0, the number 4 is 1/3 away from 1, and 5 is 1/3 away from 2. We can add those numbers to smaller circles. If two numbers are in the same smaller circle, they have distance at most 1/3 from each other.
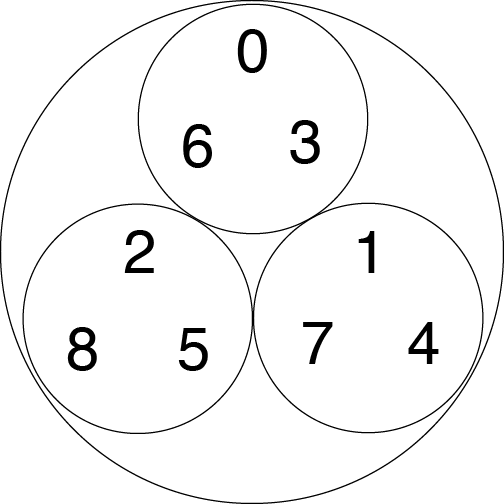
The numbers 0 through 8 arranged 3-adically. The numbers 0, 3, and 6 (for example) are all distance 1/3 from each other, so they are in the same small circle. Credit: Evelyn Lamb
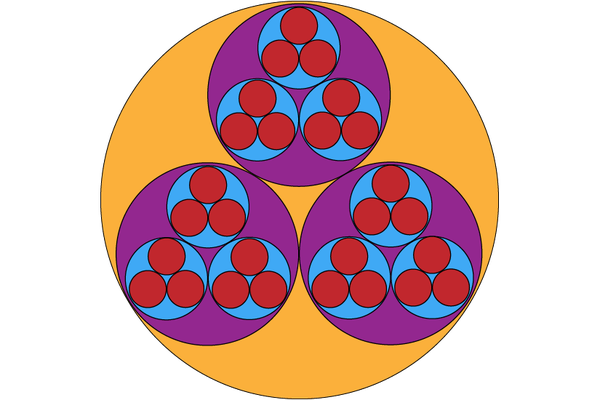
I’ll draw one more layer of this process, but we could keep going forever, yielding a lovely fractal pattern reminiscent of the Sierpinski triangle. The distance between two numbers is the size of the smallest circle that contains both of them.
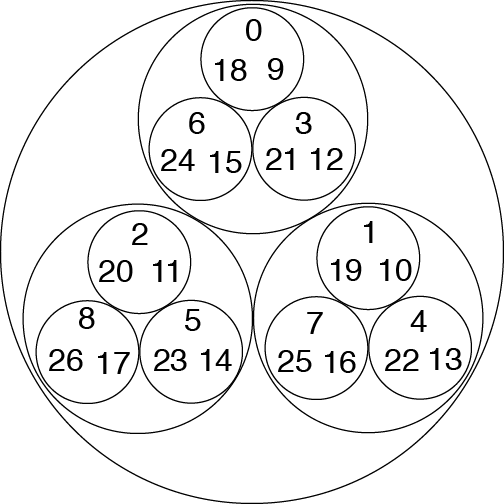
A representation of the numbers 0-26 based on their 3-adic distances from one another. Credit: Evelyn Lamb
Whew! That’s a lot of work, and we haven’t even gotten past positive whole numbers. But the p-adics don’t stop there! You can extend the p-adic absolute value and distance functions to all rational numbers.
The p-adic absolute value of a number basically measures its p-ishness. The more p-ish, the smaller the number's absolute value is. So to extend it to fractions, we want the p-adic absolute value to be small if a fraction's numerator is divisible by a power of p. To balance things out, a number to has a large p-adic absolute value if the denominator of a fraction is divisible by a power of p. (We’ll assume fractions are written in lowest terms because why would you write them any other way?) The number 1/2 doesn't really have anything to do with 3, so its 3-adic absolute value is 1. The number 3/4 has a 3 in the numerator, so its p-adic absolute value is 1/3, just like the p-adic absolute value of 3 itself. The numbers 1/3, 2/3, and 5/6 all have 3-adic absolute value 3. The numbers 1/9, 7/9, and 2/63 all have 3-adic absolute value 9, and you can see the pattern. Very large powers of 3 have very small 3-adic absolute values, and very large powers of 1/3 have very large 3-adic absolute values. We can imagine adding numbers to the p-adic diagram above. I'm not going to do it, but we could start figuring out where to add some fractions to the p-adic diagrams above. The number 1/2 is 3-adically "close" to the number 5 because 5-1/2, 4 1/2, can be written 9/2, and that has a power of 3 in the denominator.
This post is already pretty hefty, and we haven’t even gotten to how we write numbers p-adically! You’ll have to check that out elsewhere if you’re curious. You might start with these twopages from Cut-the-Knot. These p-adic expansions are very cool, conceptually related to but distinct from writing a number in base p rather than base 10. The punchline is that we get wacky things like, in 3-adic, the infinite string …222222 (infinite on the left! How exciting!) being a representation of the number -1, the infinite string …11111112 representing 1/2, and other strange delights. After figuring out how to represent all rational numbers p-adically and how to do arithmetic with them, we find that something’s missing.
Using the usual distance between numbers, we also feel like the rational numbers are incomplete. We can think of sequences of rational numbers that, when squared, get closer and closer to 2, but there is no rational number whose square is 2. We can find rational numbers that are closer and closer to the length of the circumference of a circle with diameter 1, but the number π is not rational. We can think of the real numbers as what we get when we throw in the limits of sequences of certain sequences of rational numbers (called Cauchy sequences) but don’t end up at rational numbers themselves. The technical term for this is completion. The set of real numbers is a completion of the rationals. We can do the same thing with the p-adic distance function. There are sequences of rational numbers that do not end up at a rational number in the p-adic world. We can toss in the "missing" numbers to get the full set of p-adics.
A question you might have right now is: “Why the heck would I do this?!” Constructing the p-adics is not exactly trivial or intuitive. I’ve heard several people with Ph.D.s in math say that they always have to look up the definition of p-adic numbers if they come across them. That’s definitely the case for me. There’d better be some kind of a payoff!
This question is very reasonable, and yes, the p-adics do have a good payoff. First, they allowed me to make this joke on Twitter:
The best completions of the rationals, ranked
10. you
9. can't
8. rank
7. them
6. they're
5. all
4. useful
3. and
2. beautiful
1. Reals
— Evelyn Lamb (@evelynjlamb) August 27, 2018
(There are an infinite number of completions of the rationals, but they only come in two flavors: the reals and p-adic numbers for all primes p. I like the p-adics just fine, but thinking about the p-adics is like swimming laps as hard as you can. It's a relief to sink into the warm, peaceful hot tub of the reals after a p-adic workout. Some mathematicians disagree, though. In an article for Quanta Magazine, Scholze is quoted as saying, "Now I find real numbers much, much more confusing than p-adic numbers. I’ve gotten so used to them that now real numbers feel very strange.")
The p-adics are good for more than just being months late to Twitter memes. One of the most important applications is to the problem I mentioned at the top of the post: determining whether a particular equation has any rational solutions. If a polynomial equation has rational solutions when you consider it over the real numbers, it also has solutions over the p-adics for all numbers p. That means that if you find a p for which an equation has no p-adic solution, you’ve automatically ruled out a rational solution. So if a particular equation can be easily approached via the p-adics for some p, you might be in luck. In general, though, you can just do any number-y things you want with p-adics instead of real numbers and see what happens. You can build a version of calculus using p-adics. You can build elaborate algebraic and geometric structures using p-adics. The p-adic numbers are at the root of the "perfectoid spaces" that have been an important part of Scholze's groundbreaking work. Some researchers are looking at whether the p-adics could yield fruit in physics.
Read about more of my favorite spaces: The Cantor Set Fat Cantor Sets The Topologist’s Sine Curve Cantor's Leaky Tent The Infinite Earring The Line with Two Origins The House with Two Rooms The Fano Plane The Torus The Three-Torus The Möbius Strip The Long Line Space-Filling Curves The Wallis Sieve Two Tori Glued along a Slit The Empty Set The Menger Sponge The Connected Sum of Four Hopf Links Borromean Rings The Sierpinski Triangle Lexicographic Ordering on the Unit Square The SNCF Metric The Mandelbrot Set Fatou's Pancake The Pseudosphere The Douady Rabbit The Poincaré Homology Sphere The Kovalevskaya Top A 6-Holed Torus The Real Projective Plane The 1-Dimensional Sphere The Loch Ness Monster The Koch Snowflake The Bicylinder The Catenoid SO(3) The pseudo-rhombicuboctahedron The Moser spindle The Witch of Agnesi Antoine's Necklace The Bouquet of n Circles