This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
When you look at train tracks, their parallel edges seem to converge as you gaze into the distance. But you know parallel lines remain equidistant forever. Or at least until the end of the tracks. Spaces called projective planes are mathematical models of the optical effects we see when parallel lines seem to converge.
I’ve written about one projective plane here before. It’s called the Fano plane. It’s a finite projective plane, composed of just seven points and seven lines.
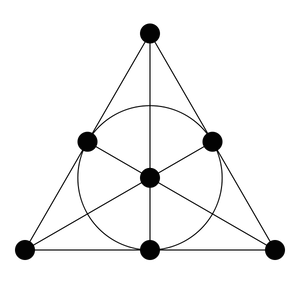
The Fano plane. The seven points are the seven large black circles. The seven lines are the six line segments that connect 3 points each, along with the circle in the middle. Credit: Wikimedia
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
It has these properties:
Every pair of points is connected by exactly one line.
Every pair of lines intersects in exactly one point.
There are four points such that no line contains more than two of them.
Anything that satisfies these rules is a projective plane, but when mathematicians refer to the projective plane, they generally mean a space more properly known as the real projective plane, or RP2. This can be defined a few equivalent ways, and looking at the different definitions can help us understand the space better.
The projective plane is one of the hardest “basic” mathematical objects for me to imagine. I’m calling it basic, even though it’s not one of the first mathematical objects you meet, because it’s one of the building blocks for other surfaces, as Emille Davie Lawrence mentioned when we talked to her for the My Favorite Theorem podcast. Despite its difficulty and abstraction, though, the projective plane had concrete origins. Those train tracks that seem to recede in the distance—how do you draw them? The seeds for projective geometry were planted when Renaissance artists started painting scenes in perspective using vanishing points, the spots on (or off) the canvas to which parallel lines would appear to converge.
Credit: Wolfram Gothe Wikimedia (CC BY-SA 3.0)
The description of RP2 that feels the closest to the artistic perspective is an example of what I think of as math by fiat. We declare it, so it is. Start with the real 2-dimensional plane. Now for each set of parallel lines on the plane, so perhaps all the vertical lines or all the horizontal lines, attach a point “at infinity” that is connected to all the lines. Now the lines intersect. To take care of the requirement that every pair of points is connected by exactly one line, we decide to call the set of all the “points at infinity” the “line at infinity.” It’s a little hard to work it out in every case, but these rules make the ordinary Euclidean plane into a projective plane. I find it hard to visualize, even though it’s the closest to the vanishing point idea. Those points at infinity are just too far away. I can’t see them.
An easier description of RP2 for me to wrap my brain around is the set of all lines through a single point in 3-dimensional space. So each line is one “point” in this space. Another way to think about that description is to imagine drawing a sphere through it somewhere. Now we can just think about the points on this 2-dimensional sphere with antipodal, or opposite, points identified because for each pair of antipodes, the same line goes through both of them. In other words, the North Pole and the South Pole are considered the same point, and so are all other pairs of points across the sphere from each other. (Curious about what place on the globe you’re antipodal to? There’s a map for that. Spoiler: it’s probably water.)
To visualize this description of the projective plane, you can imagine cutting the surface of a globe along the equator and gluing the top to the bottom just right. You want to glue, say, the north part of Ecuador, which is cut by the equator, not to the south part of Ecuador but to someplace in Indonesia exactly antipodal to it. The tough part, at least if you want to execute this global rearrangement with a real globe, is the equator itself. It needs to be wrapped around on itself so Ecuador is on top of Malaysia. As you may have guessed, it’s not possible to do this perfectly in the real world, but as mathematicians, we can just imagine that we can.
It’s not too hard to see that this description of the projective plane satisfies the three requirements above. The sphere itself comes close in the first place. There, any two points have at least one line between them, and any two lines intersect at least once. The problem is the antipodal points. The north and south poles have many lines that connect them, the lines of longitude. The projective plane takes care of that by declaring that the north and south poles are actually the same point. In general, any two great circles (lines that look like the equator or lines of longitude on a globe) intersect in antipodal points, so once we think of antipodal points as the same, we’re in the clear.
Another way to think of the projective plane is as a Möbius band with a disc glued onto it. This animation by Ronnie Brown (thanks to Tai-Danae Bradley for making me aware of it) shows how to get from the weird hemisphere description of the space to the Möbius band with a disc description. (More information here.)
Last year, I was at a conference with Stony Brook mathematician Moira Chas, who showed me this neat fabric model of the projective plane. (The idea came from graduate students at Stony Brook many years ago.) She sewed a zipper to the side of a fabric Möbius strip and to a disc of fabric. Then you can assemble the projective plane by zipping the two pieces of fabric together.

Moira Chas created this fabric model of a projective plane being assembled from a Möbius band and a disc. Credit: Moira Chas and Clara Sullivan
You can also get the projective plane from the Möbius band without the disc. You just need to glue half the boundary of the Möbius band to the other half of the boundary in just the right way. It looks a lot easier in this diagram than it is in real life. Do not attempt this with a physical object unless you have a higher tolerance for frustration than I do.

To make a Möbius band, twist the square so you can glue the sides labeled A together with the arrows aligning. Then to make the Möbius band into a projective plane, do the same things with the sides labeled B. Good luck! Credit: Wikimedia
The projective plane doesn’t quite fit properly into 3-dimensional space, as you’ll see when you try to get the fabric model to behave. The Möbius band does just fine, but when you try to glue (or zip) the disc on, it will have to intersect itself somewhere. There are a few different ways to put it into 3-dimensional space. A particularly lovely example is called Boy’s surface, named after the German mathematician Werner Boy. It is one of the smoothest possible projections of the surface into 3-dimensional space. It doesn’t have any spots where the surface is pinched, but it does intersect itself extensively.

Boy's surface rotates in space. Credit: A13ean Wikimedia (CC BY-SA 4.0)
It's hard to believe all these pictures display the same surface. Each one highlights different traits of the space. I don't quite understand the way these descriptions converge into the same space as they recede into the distance, but I know they must.
For more information on the projective plane:
A different introduction to the projective plane by Chris Lambie-Hanson Pictures of the Projective Plane by Benno Artmann (pdf) The Fundamental Group of the Real Projective Plane by Tai-Danae Bradley
Read about more of my favorite spaces: The Cantor Set Fat Cantor Sets The Topologist’s Sine Curve Cantor's Leaky Tent The Infinite Earring The Line with Two Origins The House with Two Rooms The Fano Plane The Torus The Three-Torus The Möbius Strip The Long Line Space-Filling Curves The Wallis Sieve Two Tori Glued along a Slit The Empty Set The Menger Sponge The Connected Sum of Four Hopf Links Borromean Rings The Sierpinski Triangle Lexicographic Ordering on the Unit Square The SNCF Metric The Mandelbrot Set Fatou's Pancake The Pseudosphere The Douady Rabbit The Poincaré Homology Sphere The Kovalevskaya Top A 6-Holed Torus