This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
Spouse: What is your favorite space going to be this month? Me: I don’t know yet. Any suggestions? Spouse: Well, my birthday is this month. You could do a flat surface. Me: Which one should I do? Spouse: Ooh, ooh, do two tori glued together along a slit! I love that one! Thus this month’s favorite space is dedicated to my wonderful spouse. Happy birthday!
My spouse’s research lies at the intersection of geometry and dynamical systems. Geometry is pretty self-explanatory: shapes, distances. Dynamical systems, or dynamics, is the study of spaces that change over time.
One of the types of systems my spouse studies is billiards in polygons. The prototypical example would be billiards in a rectangle, which is how the actual game of billiards is played. Mathematicians ignore the effects of friction or irregularities in the table and think of billiards in an idealized way. Instead of a ball with mass, a single point travels in a straight line until it hits the side of the table, at which point it has a perfect elastic collision with the side and continues along its way in another direction.
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
But even that is too much for mathematicians! All that bouncing around and changing directions make it too complicated to keep track of the trajectory, so they employ a clever trick to make their questions easier: they unfold the table. When the ball hits the side, instead of the ball being reflected, the table is reflected, and the ball continues unhindered. That way the direction stays the same forever. To see how this works for a rectangle, we’ll follow a point around to see what happens.
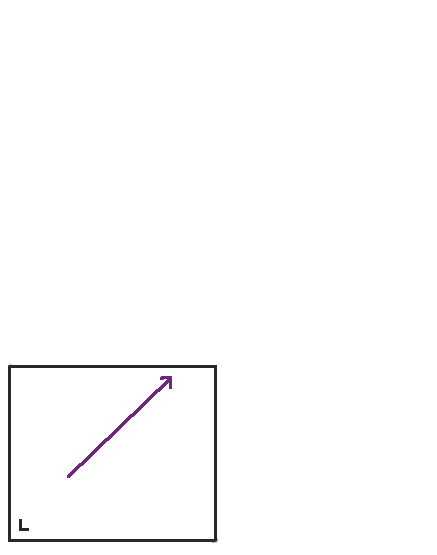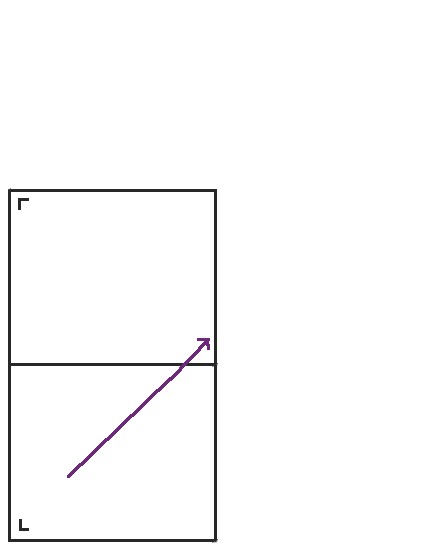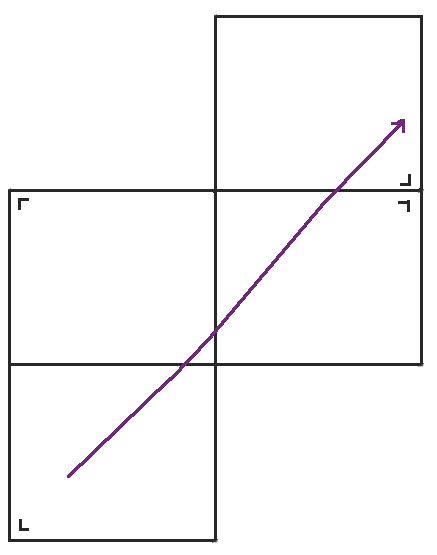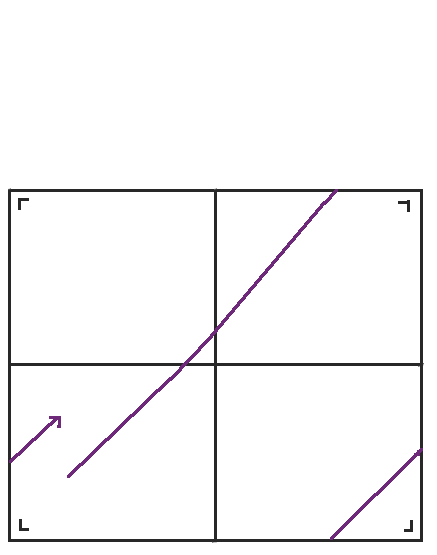
First, we start out moving northeast in a rectangle. I marked the rectangle with a little L in the bottom left corner so we can keep track of the orientation of the table as we unfold it.
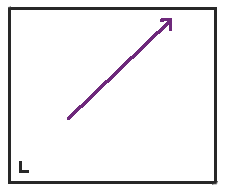
When we get to the top of the rectangle, instead of bouncing back, we reflect the table across the top, and the point continues on its way.
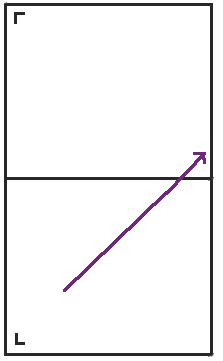
When we reach the right side of the table, we reflect the table across the right side and keep going.

When we get to the top of that table, we reflect again.
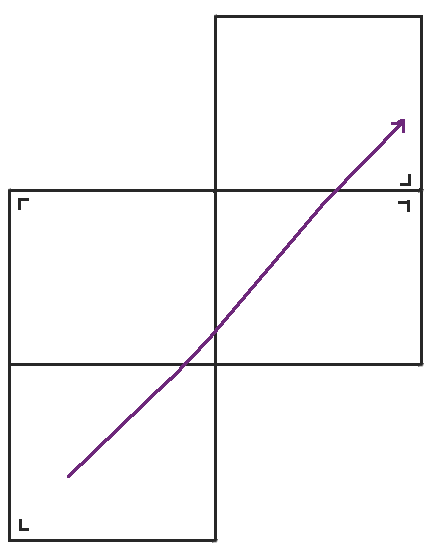
When we reach the right side, we could reflect the table again, but the bottom left table has the same orientation as the table we would get, so we might as well jump back down to the bottom left table again instead. When we rearrange the table a little bit, we get our familiar torus, a rectangle with the top glued to the bottom and the left side glued to the right side.

Here's the whole process as a gif.
In this way, billiards in the rectangle are directly related to straight line flows on a torus, which are easier to study. Northwestern University mathematician Diana Davis has a great expository paper about mathematical billiards (pdf) for more information about this relationship between billiards in polygons and straight lines on surfaces.
My spouse likes billiards on a rectangle just fine, but the behavior of trajectories there is very well understood, so he wants more of a challenge. The simplest way to complicate the surface is to add a barrier to it. Imagine that some inconsiderate person nailed their pool cue to the table, and the balls are bouncing off of that in addition to the sides.
We can do the same unfolding procedure we did with the rectangle to get this picture.
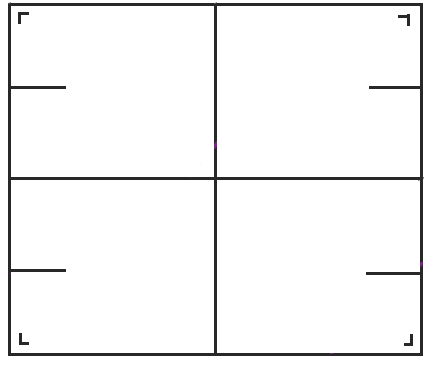
But we need to be careful now. We want the billiard trajectories all to be straight rather than bouncing around and changing direction, so when we hit the barrier, we need to jump to another copy of the barrier and continue in the same direction. In this way, it becomes something more like a slit or a wormhole—you fall in one side and emerge on the other.
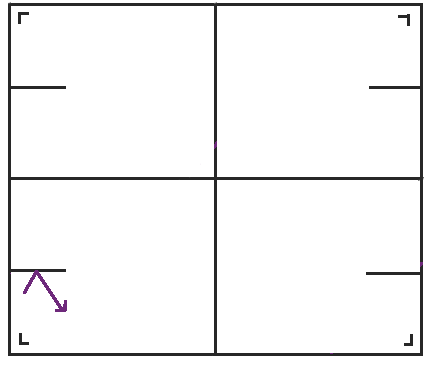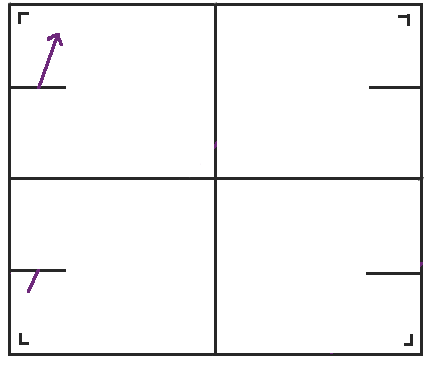
Now we have a funny predicament. We can glue the right and left sides together, no problem, but the slits separate the figure into two cylinders. I’ve shaded one blue and one orange.

At this point, we can re-conceptualize the figure entirely to get the space my spouse loves so much, the two tori glued together along a slit. The slits in the table should be glued together, making each cylinder into a monochromatic torus with part of one of the sides not actually glued together. Then you can drag the unglued parts around so they're easier to see, right smack dab in the middle of the tori. I've depicted it in 2-d as two rectangles with identification lines drawn in—you glue matching lines together—but you could also think of it in 3-d as two donuts held together by a thin line of jelly. (Or maybe I'm just hungry.)
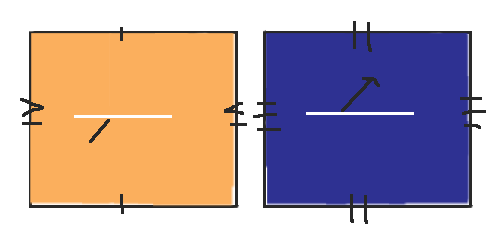
Trust me, you don't want to see my attempt at drawing this in 3-d.
Interestingly, the slit on the billiards table is a different slit than the slit on the tori! I drew the slit on the tori in white to distinguish it from the slit, or barrier, on the table. In this case, when a trajectory hits the slit on one torus, it pops out of the slit on the other torus and keeps going in the same direction. Once again the slit is like a wormhole, this time between the two tori.
Now that I’ve gone to great lengths to describe this space, what’s the point? Why would someone love two tori glued along a slit? I asked my spouse, and he said he loves it because it’s different enough from the torus, or billiards in the rectangle, to be interesting, but similar enough that some of the techniques used to study the torus are applicable there. He also told me about some of the interesting behavior mathematicians can cook up for it.
A fundamental problem in dynamical systems is how things get distributed. In the case of billiards in polygons or flows on surfaces, this means we’re trying to figure out whether the trajectory fills up the surface, and if it does, whether it fills it all up evenly, or if there are parts where it’s more or less dense than other parts.
There are two properties that are related but not quite the same that the tori glued along a slit help elucidate. The first is density. A flow is dense if it hits every rectangle in the space infinitely often, no matter how small the rectangle is. The second is uniform distribution. A flow is uniformly distributed if it hits every rectangle proportionally to its area. That is, it spends half its life in the top half of the rectangle, a quarter in the lower left quarter of the rectangle.
For the rectangle/torus with no slits, there are no dense flows that are not uniformly distributed. The two properties are equivalent in that space. But with the rectangle with a barrier, they are different. Depending on the length of the slit, some trajectories can be dense, so they hit every part of the table, but spend more time in some parts of the table than others.
When we started talking about the two tori glued together along a slit, I kept asking my spouse question after question. The more he told me, the more questions I had. Some answers are known, and some aren’t. My drawing skills aside, the slits I’ve shown here are all supposed to be exactly halfway up the side of the rectangle, so the two tori you get, the orange and the blue ones, are the same size. My spouse says if you move the slit so it’s, say, 2/3 of the way up the side of the rectangle, the behavior is unknown. So another reason I love this space is that the construction is not too difficult, but I can tweak it just a little bit and find questions that even experts in the field don’t have the answers to yet!
Read about more of my favorite spaces: The Cantor Set Fat Cantor Sets The Topologist’s Sine Curve Cantor's Leaky Tent The Infinite Earring The Line with Two Origins The House with Two Rooms The Fano Plane The Torus The Three-Torus The Möbius Strip The Long Line Space-Filling Curves The Wallis Sieve
