This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
Ah, the humble torus: the beginning topologist’s friend and manifestation of the gap between theory and practice. The torus has many lives and shows up all over the place in mathematics.
First, it has a topological life. Topology doesn’t care exactly what you look like, it just cares about large-scale features. Specifically, it cares about aspects of an object that stay the same as it is stretched or squished, as long as there is no tearing. In the topological world, a torus is a two-dimensional space, or surface, with one hole. (To be a bit fancier, it is an orientable surface of genus one.) Topologists, eager to associate themselves with the more immediately appealing subject of pastry, describe the torus as a donut, although to be annoyingly precise, it is just the glaze. (The bread of the donut is a three-dimensional space called a solid torus.)
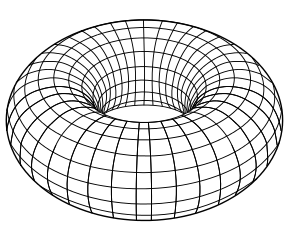
Image: public domain, via Wikimedia Commons.
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
Often, we represent the torus as a nice plump donut, but topologists are also partial to a more abstract way of portraying it. In this picture, we draw it is as a rectangle with a few markings called identifications.
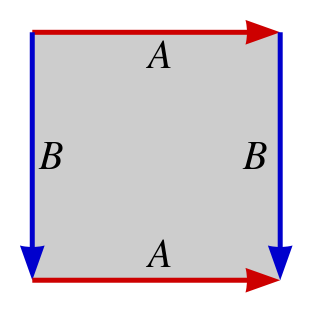
The arrow marked "A" at the top is glued to the arrow marked "A" at the bottom, and the arrow marked "B" at the left is glued to the arrow marked "B" at the right. Image: public domain, via Wikimedia Commons.
As in the classic computer game Asteroids, when you travel up through the top of the rectangle, you reappear at the bottom, and traveling through the right side causes you to rematerialize on the left. This drawing, though not quite as appetizing as the donut, still shows us all the important topological properties of the torus.
The flat rectangle picture also serves as a nice segue into another one of the torus’s lives, its life as a geometric object. In contrast to topology, geometry does care about exact shapes and distances. The plump torus and the skinny one are topologically the same but geometrically different.
Geometers care about the rectangle picture of the torus because it is a finite surface that is fundamentally flat, just like the infinite plane. If you’ve ever had the jarring realization that Greenland is 7% of the size of Africa, not practically the same size, you are secretly aware of the fact that the sphere can’t be flattened out onto the plane in a way that preserves distances. That’s because it’s positively curved, and the plane is flat. There are also negatively curved surfaces, and they also can’t be flattened onto the plane without some distortion either.
The rectangle picture of the torus is a demonstration of the fact that the torus is flat. It would be awfully nice, then, to be able to see it as a flat surface in three dimensions rather than just drawing it on paper and using our imaginations. We can try to do this by performing the identifications in the rectangle picture. We start with a rectangle.
.JPG?w=300)
The first gluing takes us from flat piece of paper to cylinder.
.JPG?w=300)
The second gluing brings the ends of that cylinder together.
.JPG?w=300)
There’s the rub. Assembling this torus did not go as well as planned. It’s a crumpled collision of theory and practice.
.JPG?w=300)
#sadtorusselfie
No mathematical object is perfect when it enters the real world. Any circle we draw is not quite ideal, and the surface we draw it on is not truly a two-dimensional object. But with some care and a good compass, we can make a circle that are close enough for our purposes. The torus, on the other hand, is kind of a nightmare.
So, can we ever hope to situate the torus in three-dimensional space so that no distances are distorted?

Based on a public domain image, via Wikimedia Commons.
We can do it! But it’s not as simple as you might hope.
One option is to give up on the surface being nice and smooth. In the plane, the rectangle doesn’t have any creases, but if we throw a few in, we can get things to work. There are a lot of ways to make this happen. I made one a couple years ago.
.jpg?w=300)
And mathematical 3-D printing wizard Henry Segerman has a nice example where the ridges are hinged.
What if I want more? What if I want to eliminate those jarring, unsightly creases? Well, we can have that too! But it gets a bit complicated. In 2012, Vincent Borelli, Saïd Jabrane, Francis Lazarus, Boris Thibert, and Damien Rohmer published the first pictures realizing the flat torus in 3-space without any jagged corners. They write, "The images reveal an unexpected object, halfway between fractals and ordinary surfaces: a smooth fractal." In other words, they combined the infinite nature of fractals with a smoothing process to avoid sharp ridges.

Image: Borelli, Jabrane, Lazarus, Thibert, Rhomer, in their PNAS paper.
In the end, the “flat” torus looks anything but flat, but it manages to satisfy the letter of the law. All the distances are exactly what they are on the rectangle in the plane. For more about this smooth fractal torus, see this detailed article by Lê Nguyên Hoang, this article and video by Christian Lawson-Perfect of the Aperiodical, or the Numberphile video on the subject.
The torus has many other lives: in topology, it is one of the first examples of a product space and a useful first try at using the Seifert-van Kampen theorem. In dynamics, it is one of the first translation surfaces a student encounters and plays pool in. In my field, Teichmüller theory, it is one of the only surfaces that is simple enough that you can really understand and compute its Teichmüller space. In general, it seems that the torus is often the example that is worth a thousand theorems when encountering a new idea. In the spirit of the Thanksgiving season, let's take a moment to thank the torus for being a helpful example to have at our fingertips whenever two-dimensional geometry or topology crop up. (After all, math is always better over an orientable genus one pastry.)
Read about more of my favorite spaces: The Cantor Set Fat Cantor Sets The Topologist’s Sine Curve Cantor's Leaky Tent The Infinite Earring The Line with Two Origins The House with Two Rooms The Fano Plane The Three-Torus The Möbius Strip The Long Line Space-Filling Curves