This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
As I was going to St. Ives,
I met a plane with seven lines,
Each line had
seventhree points,
(But there were seven points in total),
This poem doesn’t work very well for the Fano plane.
I humbly propose that the Fano plane is the smallest interesting space. There may be a cheeky inductive proof to the contrary, but a single point, or a few isolated points, do not an interesting example make.
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
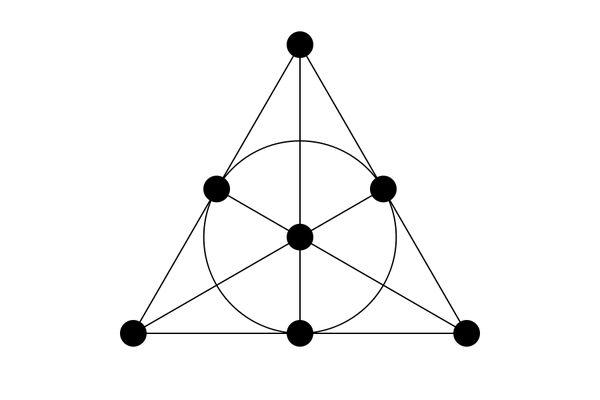
The Fano plane has seven points that lie on seven lines. That’s it. It is the smallest possible example of a projective plane.
Have you ever thought it was kind of a bummer that some lines in the plane intersect, but some don’t? How arbitrary! Projective planes allow you to smooth out this irritating problem by forcing lines to intersect.
To be a projective plane, a few conditions must be satisfied.
Every pair of points is connected by a line.
Every line intersects every other line.
There are four points such that no line contains more than two of them. (This third condition is not always listed, but it rules out silly cases such as 2 points on one line or several lines that go through one point.)
Sometimes math is about mind over intuition, and some of those times are when you're thinking about projective geometry. (To be fair, sometimes projective geometry seems very intuitive; after all, one of its applications is in perspective drawing.) You can make the Euclidean plane into a projective plane by adding a point "at infinity" to every set of parallel lines. So there's a point at infinity for the horizontal lines, a point for the vertical lines, a point for the lines at an angle of 47.322 degrees counterclockwise from horizontal, and so on. Then you declare the collection of points at infinity to be the line at infinity. If you think for a while, you can convince yourself that this satisfies all the requirements.
If infinitely many points on the line at infinity are too rich for your blood, the Fano plane is a less expensive alternative. It's easy to see exactly how the points and lines intersect and interact.
The Fano plane challenges the intuition. When you see a picture of it, you will very understandably think it has infinitely many points. After all, it has 7 lines, and we all know a line segment, even a very short one, has infinitely many points on it.
No! Math is a dictatorship, and we are the dictators. We declared that the seven points were the only seven points. Lines aren’t made of points, they’re just lines. Another counterintuitive aspect of the Fano plane is that one of those lines looks like a circle, at least in most portrayals of it. But if you’ve already gotten on board with the idea that lines aren’t made of infinitely many points, it shouldn’t be too hard for you to convince yourself that the circle is really a line.
The Fano plane is the smallest finite projective plane. You might wonder how large other projective planes are. If we want to have 4 points on each line instead of 3, can we find one? It's surprisingly nontrivial to figure out how large a projective plane can be. (A note on nomenclature: the Fano plane is said to have order 2 because each line has 2+1=3 points on it and each point is on 2+1=3 lines. In general, a projective plane has order N if each line has N+1 points and each point is on N+1 lines. A projective plane of order N has N2+N+1 points.) We know there are projective planes of every prime order and every order that is a power of a prime, but for other numbers, we still have a lot of work to do. Only in the nineties did researchers conclusively prove that there is no projective plane of order 10 (pdf), for example, and the question is still open for 12.
Although finite projective planes seem like a triumph of purely axiomatic thinking over any hint of reality, the Fano plane and its relatives have some surprising applications to gambling, of all things. I first read about them in Jordan Ellenberg’s book How Not to Be Wrong. He gives an example of a lottery where 3 numbers are picked of 7 total. A player wins the jackpot by matching all 3 of them or a less extravagant prize for picking 2.
There are a total of 35 possible combinations of 3 numbers out of 7, so you only have a 1 in 35 chance of getting the jackpot. But you can improve your chances of matching 2 with the help of the Fano plane. The trick is to buy a few cards and to avoid having the same pair of numbers on any two cards. You don’t want to buy both 123 and 234 because if two of the numbers are 2 and 3, you’ve covered it twice. That means twice the prize, but it also means you won’t get anything for a different pair.
To win the lottery with the Fano plane, label each point with a number from 1 to 7 and read off the numbers on each line. I got 123, 147, 156, 246, 257, 345, 367.
If you check these numbers, you’ll find that every pair is represented exactly once. No matter what the jackpot is, we will match at least two of the three numbers. If you labeled your points differently from the way I did, you’ll get a different collection of numbers, but it will still have the same property.
There aren’t many lotteries that draw only 3 numbers, but with some care and computer power, the idea can be scaled up. Of course, it is very unlikely that a lottery payout system would be lucrative enough to justify even a clever strategy involving projective planes, but if you’re interested, Ellenberg relays the story of Cash WinFall, whose prizes were just good enough to win some MIT students some real money.
To learn about connections between the Fano plane, Latin squares, torus topology, error-correcting codes, and many other topics, check out these two articles by Ezra Brown of Virginia Tech: The Many Names of (7,3,1) and Many More Names of (7,3,1). The Fano plane can also help you remember how multiplication works in the octonions if that's your jam, and I can't help but point out that it bears a striking resemblance to the symbol for the Deathly Hallows.

Axiomatic geometry has little to say about stone, wand, or cloak. Image: Public domain, via Wikimedia Commons.
Read about more of my favorite spaces: The Cantor Set Fat Cantor Sets The Topologist’s Sine Curve Cantor's Leaky Tent The Infinite Earring The Line with Two Origins The House with Two Rooms The Torus The Three-Torus The Möbius Strip The Long Line Space-Filling Curves