This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
I can’t think about the house with two rooms without hearing John 14:2: “In my father’s house there are many rooms.” This topological example is a bit more modest than the kingdom of God. After all, there are just two rooms. A more appropriate verse is this: In Bing’s house, there are two rooms. If it were not so, would Hatcher have told you how to construct it?
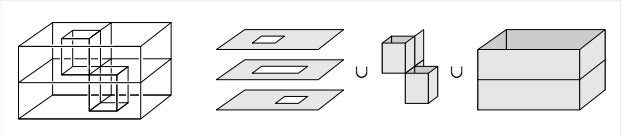
The house with two rooms is sometimes called Bing’s house after R. H. Bing, the mathematician who first described the space. But like many math students, I first encountered it in Allen Hatcher’s algebraic topology book. He gives us the following picture and definition of the space.
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
To build this space, start with a box divided into two chambers by a horizontal rectangle, where by a ‘rectangle’ we mean not just the four edges of a rectangle but also its interior. Access to the two chambers from outside the box is provided by two vertical tunnels. The upper tunnel is made by punching out a square from the top of the box and another square directly below it from the middle horizontal rectangle, then inserting four vertical rectangles, the walls of the tunnel. This tunnel allows entry to the lower chamber from outside the box. the lower tunnel is formed in similar fashion, providing entry to the upper chamber. Finally, two vertical rectangles are inserted to form ‘support walls’ for the two tunnels. The resulting space X thus consists of three horizontal pieces homeomorphic to annuli plus all the vertical rectangles that form the walls of the two chambers.
If your eyes glazed over a bit there, you’re not alone. The picture and description are hard to parse. Before we try to understand the space itself, we should figure out why we would bother with it at all. Hatcher uses it as an example of a space that is “contractible but not in any obvious way.”
“Contractible” is topological shorthand for “like a point” or, not to put too fine a point on it, “boring.” A space is contractible if it you can smush it down to a point without tearing the space or gluing any parts of it together. For example, a solid ball is contractible because even though it is three- rather than zero-dimensional like a point, it can be shrunk down all the way to a point without tearing or collapsing any of its interesting features. Hence, for some topological purposes, it’s close enough to being a point that we might as well assume it is.
Hatcher is asserting that the house with two rooms, like a solid ball, is also equivalent to a point, although less obviously so. The house is a façade. It looks as though it has holes in it, but they are not really there in a topological sense.

A bird's eye view of a house with two rooms while it is under construction. Here, only the first floor has been built.
I was skeptical of the house with two rooms for a long time. I just couldn’t see how to squish it up into a point without changing its topology. I took Hatcher’s word for it, but it wasn’t until I made it for myself that I truly believed in its contractibility. The day before spring break last semester, I brought some clay to my topology class, and one of the things we made was the house with two rooms. By the time we were finished, I felt like I truly understood the space.

The house with two rooms...and a slightly leaky roof.
Here is where I could tell you how I saw that the space was contractible, but I’m not going to do that. I think the best way to see it is to make it out of clay or any pliable material you have on hand. Hatcher’s diagram and description give a good recipe, and I know from personal experience that undergraduates and even postdocs like me can follow the instructions well enough to create a convincing house with two rooms, although I must admit our roof was leaky.
If you want to take the easy way out instead, 12-year-old David Hitchman, son of University of Northern Iowa mathematician Theron J. Hitchman, made a fun video about building it in Minecraft, and Ken Baker wrote about it on the blog Sketches of Topology. There, he describes it in a different way:
You know how instead of doing a handshake, you could grab each other’s wrists? And your thumbs almost but don’t quite reach your fingers? Bing’s glove for two hands would fit snugly.
Apparently the house with two rooms (or the glove with two hands, as I may have to start calling it) inspires religious thoughts in me. As I was writing this post, I realized that like doubting Thomas, I needed to feel the space with my hands before I would believe it. “Because you have seen me, you have believed; blessed are those who have not seen and yet have believed.” Jesus’ reply to Thomas may work for discipleship, but I think it’s backwards for topology. Blessed are those who have to get out some clay or open Minecraft and create the house with two rooms before they believe in it.
Read about more of my favorite spaces: The Cantor Set Fat Cantor Sets The Topologist’s Sine Curve Cantor's Leaky Tent The Infinite Earring The Line with 2 Origins The Fano Plane The Torus The Three-Torus The Möbius Strip The Long Line Space-Filling Curves