This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
In the Star Trek: The Next Generation episode “Where Silence Has Lease,” the Enterprise flies into a void. Trying to get out, they set a stationary beacon down (never mind what it would mean for the beacon to be stationary in space or how you’d get it to stay there) so they can better measure how far they have gone. As they fly away, the beacon gets farther from them until it starts to get closer. Eventually, they return to where they started.
The Enterprise didn’t do enough exploration of the void for us to know for certain, but it’s quite possible that they had accidentally wandered (or the godlike being Nagilum had pulled them) into a three-torus. Like the two-dimensional torus, which can be represented as a square with opposite sides glued together, the three-torus can be represented as a cube with opposite faces glued together. When you move forward or to the side, you eventually reappear on the opposite face of the cube. When you move up, you eventually reappear at the bottom of the cube.
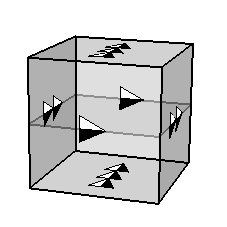
The cube model of the three-torus. We imagine gluing together the matching arrows, so the front is glued to the back, the left to the right, and the top to the bottom. Image: UIUC.
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
The two-torus is easy to picture in many different configurations, but the three-torus is harder to visualize. With the two-torus, the square picture is somewhat helpful, but the donut picture gives me a better feel for what it would really be like to live on a torus. For the three-torus, I don’t have access to enough dimensions of visualization to see it holistically like that. I can try by mentally gluing faces together one at a time. First, the top face is glued to the bottom face, making a solid torus with a square cross-section (a square donut, basically). Then we glue the left to the right, which ends up looking like a donut with part of the inside devoured. But the next step is to glue the inside to the outside. This doesn’t work so well in three dimensions.
Often, when a topologist or geometer is asked about applications of her research, she’ll mumble something about the shape of the universe before trying to distract the other person with a pretty picture of the Poincaré disk. (Or is that just me?) But the three-torus may actually have something to do with the shape of the universe. Topology and geometry give us ways to classify all possible three-dimensional shapes, also called three-manifolds. Depending on what properties we can determine that the universe has, we can narrow down the options for the shape of the universe.
I’m not an astrophysicist, and I’m not up to date on the latest measurements that might help us determine the shape of space, so I don’t know what the current thinking on the shape of the universe is. But what if it is a torus? An alternative visualization of the three-torus shows us how weird that would be.
.png?w=238)
Another visualization of the three-torus. I like to call this one an infinite scaffold. For larger image, click here. Credit: Jeff Weeks.
This infinite scaffold distorts one important feature of the three-torus: the three-torus is finite, while this picture looks infinite. But it sheds more light on how disorienting it would be to live in a torus.
Once again, let’s back up a dimension and think about the analogous picture for the two-torus. This would be an infinite grid on a plane rather than just one square. We’d just keep in mind that points that were in the same relative position in two different squares in the plane were actually the same point.
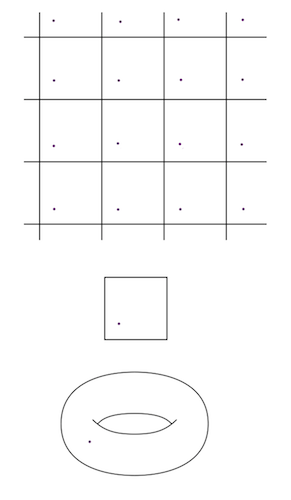
A torus with a lovely beauty mark portrayed in three different ways. The top is as an infinite lattice. Each square is really the same square. The middle is just one square (with opposite sides mentally glued together). The bottom is its realization as a donut-shaped surface.
If you lived in a torus (two- or three-dimensional) and looked out from one point, your line of sight might wrap around the torus several times.

A line emanating from a point in the torus, portrayed in three different ways. I drew this in a two-torus instead of a three-torus because my illustration skills only go so far, but you may be able to imagine a similar thing happening in the infinite scaffold picture of the three-torus.
If you looked straight up from a point in the three-torus, you’d see the bottom of your own feet. Depending on your angle and visual acuity, your line of sight could theoretically wrap around the torus infinitely many times. If you looked around, you'd see infinitely many copies of yourself. It’s a narcissist’s dream.
If we do live in a three-torus, of course, it is a bit too big for us to see our own rear ends, which is a relief. I wonder, though, if we'll ever know for sure what manifold we inhabit.
Read about more of my favorite spaces: The Cantor Set Fat Cantor Sets The Topologist’s Sine Curve Cantor's Leaky Tent The Infinite Earring The Line with Two Origins The House with Two Rooms The Fano Plane The Torus The Möbius Strip The Long Line Space-Filling Curves