This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
On Sunday, I wrote about my public statistics session at ScienceOnline. Today, I'll tell you a little about my other session, Hands-on Math, co-moderated by Matthew Francis. If you come to our session, you might get to take home a mathematical surface of your very own.
Meet Ellie. She may look like an oddly shaped pillow, but she is much, much more.

Ellie, a surface of genus 2. More pillows should have genus. Credit: Evelyn Lamb
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
In the first place, Ellie is a surface with genus 2. She has two holes, which you can see a little better in this picture.

A top-down view of Ellie, demonstrating the fact that she does indeed have genus 2. Credit: Evelyn Lamb
Surfaces show up all over the place in mathematics, and Ellie is a very interesting surface with a lot of properties to explore. For example, she is a translation surface. These surfaces are formed by taking a polygon in the Euclidean plane, in this case an L-shaped piece of fabric, and gluing (or sewing) parallel sides of the same length together.

An L-shaped piece of fabric labeled with identifications to make it into a translation surface. Edges with the same symbol will be sewn together. Credit: Evelyn Lamb
I'll let Diana Davis's "Dance Your Ph.D." video explain it another way.
Cutting Sequences on the Double Pentagon, explained through dance from Diana Davis on Vimeo.
In the first scene, whenever the dancer crosses one of the edges of the double pentagon, she re-emerges in another part of the screen because we are to imagine that the figure is glued up, with sides of the same colors identified.
Translation surfaces are just fun to play with on their own, but they also arise naturally when we study billiards on polygons. For example, in an L-shaped billiard table, what kinds of trajectories can the cue ball take? Believe it or not, we can study surfaces like Ellie to find out. By the way, this is not an entirely academic exercise: mathematician Moon Duchin actually came across one of these L-shaped tables on a trip to South Africa.
A plain old single-holed torus is another example of a translation surface. The polygon in that case is a square or rectangle.
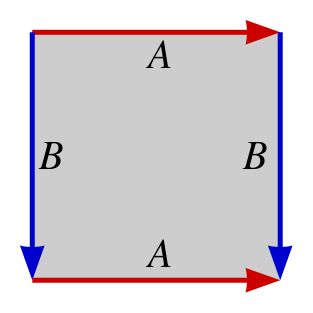
A square with top and bottom sides labeled "A" and right and left sides labeled "B." Make a torus by gluing sides with the same labels together with arrows lining up. Credit: Ilmari Karonen Wikimedia (public domain)
This animation shows the gluing process:

A square rolls up into a cylinder and then a torus. Credit: LucasVB Wikimedia (public domain)
We can see that no matter where we stand on the torus, the ground is very smooth around us. That's because if we look at what happens to the corners of the square, they are all identified together, but there is exactly 360° of angle around them. With the L-shaped table, this is a little different. Once again, all of the corners are identified to the same point, but now we have way more than 360° around that point.

When the identifications are made, the blue vertices all end up being identified as the same point. The green arcs around the blue points help us count the amount of angle around this point. Here we can see that we have three circles' worth, 1080°. Credit: Evelyn Lamb
That funny point, which is hard to photograph, is often called a cone point. I made Ellie because I wanted to have a touchable model of a surface that is kind of like the surfaces I study, which have these funny cone points. She is not exactly the same as my surfaces because her skin is modeled on the boring Euclidean plane rather than the sexier hyperbolic plane that I work with. But I don't have any vast sheets of fabric made from hyperbolic crochet, and the hyperbolic surfaces wouldn't fit into 3-dimensional space properly anyway, so Ellie is the closest thing I have.
Which brings us back to the purpose of this post: to invite you to the fun world of math you can make and touch at our hands-on math session. We'll be talking about some of the subjects I've brought up here: topology, geometry, and dynamical systems, and we'll be making surfaces from fabric and paper. Matthew is a physicist, and he'll introduce some of the ways these mathematical concepts come up in physics.
If you think you might come to the session, we would really appreciate it if you could let us know on the wiki. I know these decisions are often made at the last minute, and that's totally fine. But a general idea of the number interested will help us with bringing the right amount of fabric. If you can't come, you can follow us on Twitter by using the hashtag #HandsOnMath.