This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
I had never heard of the Wallis sieve until a couple weeks ago, but it quickly claimed a place on my list of all-time favorite spaces. I found out about the space from this video by Matt Parker.
Parker never identifies the Wallis sieve by name, but it’s there. The Wallis sieve is a fractal-like object that’s easiest to explain by starting with a Sierpinski carpet. A Sierpinski carpet is a 2-dimensional fractal somewhat analogous to the Cantor set, which I wrote about last year. To make one, take a square with side length 1, divide it into 9 smaller squares, and remove the middle one. Then divide each remaining square into 9 smaller squares and remove the middle one, and so on.
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.

Six stages in the construction of the Sierpinski carpet. Image: KarocksOrkav, via Wikimedia Commons. CC BY-SA 3.0.
The Wallis sieve starts the same way as the Sierpinski carpet: take a square of side length 1 and remove the middle ninth. Then things get funky. Instead of removing the middle ninths of all the remaining squares, we divide each of those squares into 5×5 grids instead of 3×3 and remove the middle square of each one, which ends up being 1/25 of the total area. In the next step, we divide all of the remaining squares into 7×7 grids and remove the middle square, or 1/49 of the remaining area, from each one.

Four stages in the life of the Wallis sieve. Image: Evelyn Lamb.
Whereas with the Sierpinski carpet, we always removed 1/9, with the Wallis sieve we remove a smaller proportion of the remaining set each time. The Sierpinski carpet ends up having zero area in the end, just like the Cantor set, but the Wallis sieve has a positive area, like a Cantor set that's been fattened up a bit.
Before I get my hands dirty with some computations, though, I should note that there is a little bit of ambiguity about what exactly the Wallis sieve is. The figure I described has an area of π/4, the same as a quarter of a circle with radius 1. Some people find it more satisfying to stick four of them together to get an area of π, or a whole unit circle, and call that figure the Wallis sieve. I’ll stick with my earlier definition in this post.
Either way, the area of the Wallis sieve is closely related to the area of a circle. Why? It all boils down to the Wallis product. English mathematician John Wallis derived this curious formula in 1655:
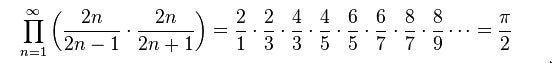
At first glance, this product doesn’t seem to have much to do with the Wallis sieve, but let’s rewrite it. We’ll ignore the 2/1 at the beginning and pair up the rest of the terms. We get 2/3×4/3=8/9, 4/5×6/5=24/25, and so on. When we look at the product this way, the Wallis sieve falls out.
In the first step of creating the sieve, when we took away the middle ninth of the square, we were left with an area of 8/9. Then when we removed the middle 25ths of the remaining squares, we were left with 24/25 of the remaining area, giving us a total area of 8/9×24/25. Then we removed the middle 1/49 of each remaining square, and were left with 48/49 of the remaining area, or 8/9×24/25×48/49 of the original square. In total (and taking into account the 2 we ignored earlier), we find that the Wallis sieve has an area of π/4, the same as a quarter of a circle with the same radius as the side length of the sieve.
I wondered whether there might be an easy way to see that the Wallis sieve is so closely related to the circle. Namely, if you squish all the white space out, do you get a quarter circle? I imagined pushing everything toward the lower left corner.
An animation showing three stages of the Wallis sieve along with a visualization of what would happen if we squished everything towards the lower left corner of the square. Image: Evelyn Lamb, with the assistance of Desmos.
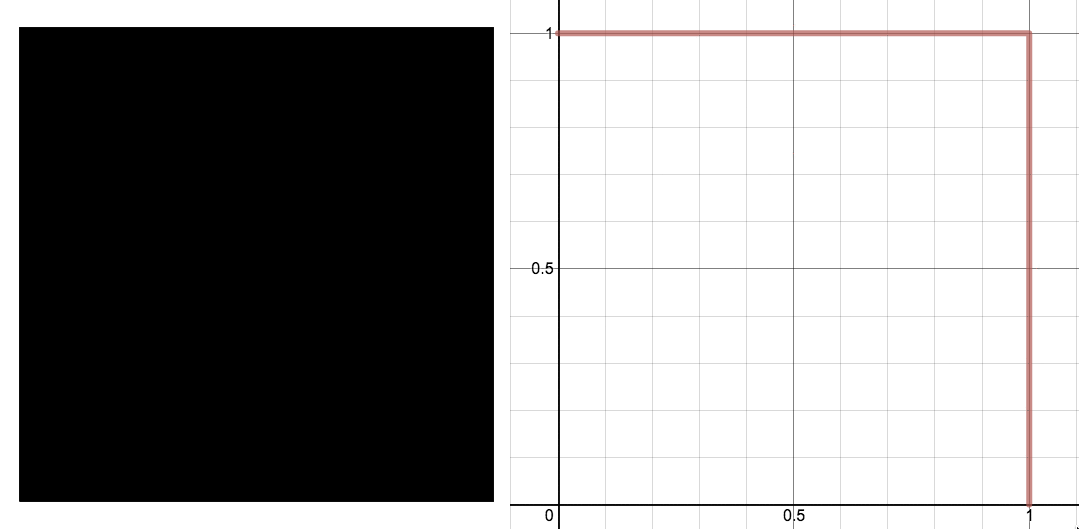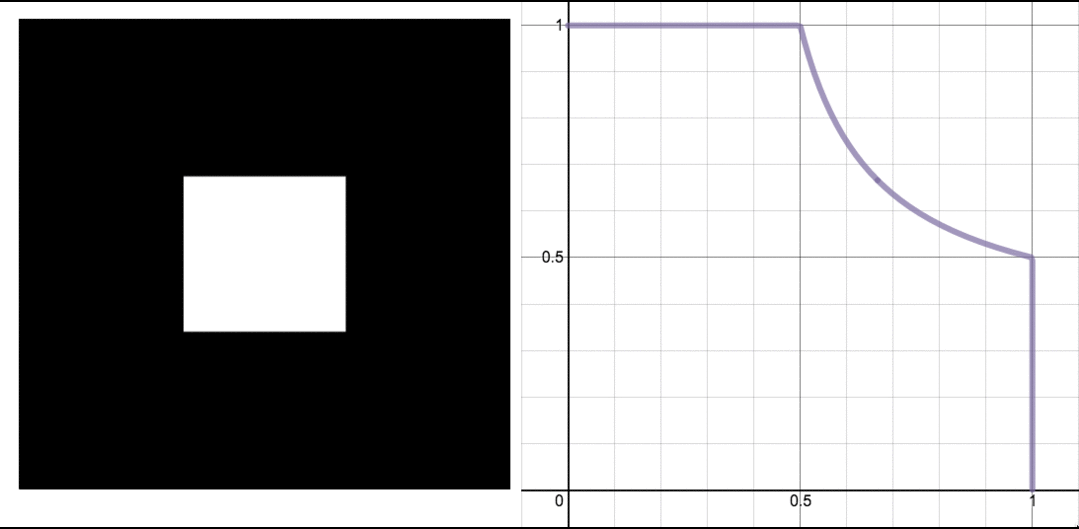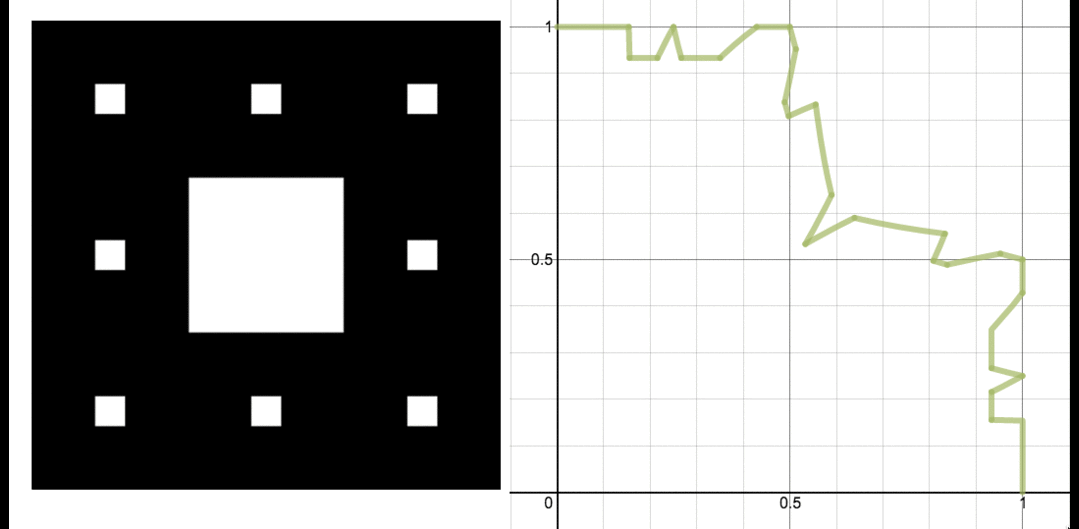
Sadly, my hopes of an easy explanation were immediately squelched: the first step, removing the middle ninth, removes enough length in some places that there’s no hope of ending up with something circular at the end.
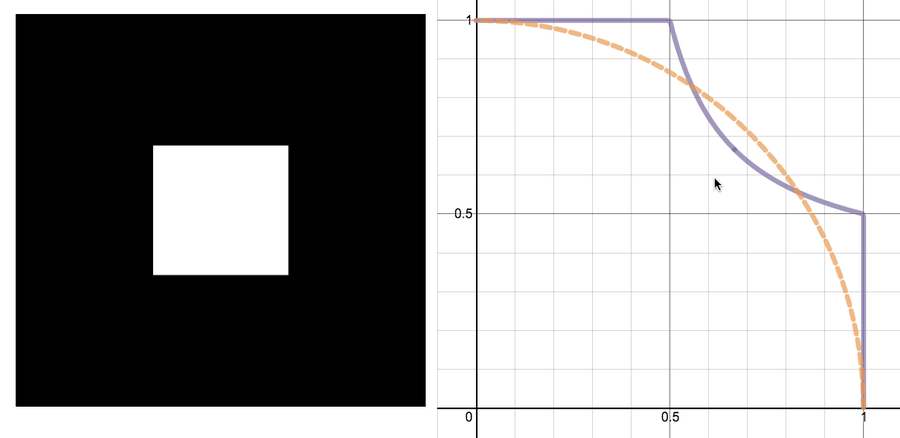
Left: a square with the middle ninth removed. Right: graph showing the result of squishing the square down and towards the left (solid purple curve) versus a wedge of a circle (dashed orange curve). Image: Evelyn Lamb.
I’m left with more questions than answers about this funny little shape. Is there an easy way to see that its area should be the same as a quarter circle? What would it look out if I squished it all the way down? Would the boundary have a finite length, or would I end up with something more like the Koch curve? And we haven’t even gotten to the 3-dimensional version yet! As Parker’s video at the top of the post notes, a similar construction in 3 dimensions gives us something with the same volume as a unit sphere! Can we do the same thing in higher dimensions?
I hope the Wallis sieve and related questions nerd snipe you as much as they nerd sniped me. If you’re hungry for more, Ed Pegg’s article “Squeezing pi from a Menger sponge” and Mike Lawler's blog posts about sharing the Wallis sieve with his kids are good jumping-off points for your own explorations.
Read about more of my favorite spaces: The Cantor Set Fat Cantor Sets The Topologist’s Sine Curve Cantor's Leaky Tent The Infinite Earring The Line with Two Origins The House with Two Rooms The Fano Plane The Torus The Three-Torus The Möbius Strip The Long Line Space-Filling Curves
