This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
This April, I finally read Watership Down for the first time, one of my book groups discussed The Year of the Hare (an odd little book by Arto Paasilinna that I found hilarious but most of the rest of my group didn’t like), and of course it was Easter, whose secular observances center around rabbits who for some reason lay eggs. What better way to get into the leporine spring spirit mathematically than to get to know the Douady rabbit?
Like many of my recent favorite spaces, the Douady rabbit is a fractal named for a Frenchman (e.g. Fatou’s pancake and the Mandelbrot set). Its eponym Adrien Douady (1935-2006) studied complex dynamics and the Mandelbrot set, which he named in honor of Mandelbrot. I don't know who decided to name this fractal after Douady, but it must have been somebunny who admired him very much.
To understand the Douady rabbit, we’ll want to start with the relationship between the Mandelbrot set and many, many Julia sets. I wrote about this relationship in my posts about the Mandelbrot set and Fatou’s pancake, but if you don’t want to go read up on those, the big idea is that every point c in the Mandelbrot set is related to a function of the form f(z)=z2+c and that we care about what happens as we iterate these functions. You plug the number z=0 in to start and then plug the output back into the function and so on. If the iterates stay bounded, the number c is in the Mandelbrot set. If the iterates grow very large, the number c is not in the Mandelbrot set.
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
The more you study and play with the Mandelbrot set, the more you’ll see that this shape is far more than a pretty piece of math that makes a good nerdy tattoo. There are many beautiful connections between the Mandelbrot set and other related fractals called filled Julia sets. The filled Julia set of a function is the collection of points whose iterates stay bounded under iteration, and the Mandelbrot set corresponds to numbers c for which the filled Julia set for the function f(z)=z2+c comes in just one piece, rather than being a scattered, dust-like object. (A dust bunny, perhaps?)
I imagine each point in the Mandelbrot set holding up a little sign with its filled Julia set painted on it. If you pick out a point in the Mandelbrot set, you know its will be carrying a sign that has a filled Julia set in just one piece, and if you pick up the signs of two nearby points, they probably won’t look too different.
The Douady rabbit is the filled Julia set for the function f(z)=z2+c, where the parameter c is approximately -0.12256+0.74486i. (Here, as usual in my posts, i=√-1.)
Whenever I write about the Mandelbrot set or related fractals, I have to plug Holly Krieger’s Numberphile video about it. Today I also want to plug the second part of the video, in which she shares more information about filled Julia sets and mentions the rabbit and some of its kin.
Aside from the fact that it looks vaguely like a rabbit — and let’s be honest: its resemblance to any lagomorph is impressionistic at best — why care about this particular Julia set? I have no problem with the mathematical equivalent of finding shapes in the clouds, but is there any reason this filled Julia set, in the vast sea of filled Julia sets, is special enough to deserve its own name?
Yes and no. The Douady rabbit has a cycle of three points, starting with 0, that map to each other under the function f(z)=z2+c for the special c that defines the map. In fact, that’s how we can figure out precisely what c is. If we start with 0 and iterate the function, plugging our answer back in, we want a cycle of points so that 0 goes to the first, which goes to the second, which goes back to 0. We know that when we plug 0 into the function f(z)=z2+c, we get c out. Then when we iterate it, plugging c in for z, we get c2+c. When we plug that back into the function, we get (c2+c)2+c, and because we want the cycle to close up, we set this number equal to 0. A little trip to an online equation solver (because who has time to memorize the cubic equation, even if it is lovely in terza rima?) and we find that c can be approximately -1.7549, -0.12256+0.74486i, or -0.12256-0.74486i. It happens that the Douady rabbit corresponds to c=-0.12256+0.74486i.
So when we fix that c and look at the function f(z)=z2+c, we know the numbers 0, c, and c2+c form a nice little loop, hopping from one to another. It happens that all the other numbers in the rabbit are attracted to this little cycle too. That cycle of points is at the heart, mouth, and ear of the rabbit (at least how I imagine the rabbit; its anatomy is open to interpretation).
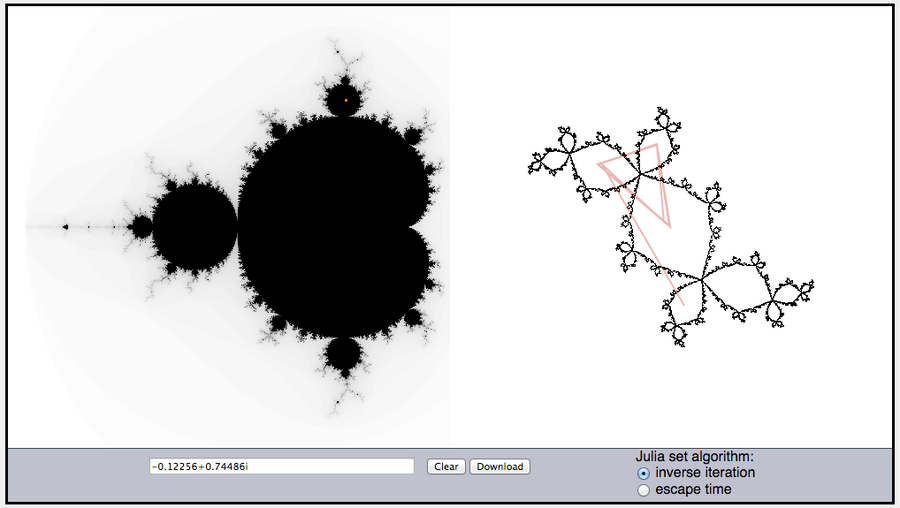
Left: The Mandelbrot set with a small red square at the point c=-0.12256+0.74486i, which corresponds to the Douady rabbit. Right: The Douady rabbit with a few red line segments showing the trajectory of a point under the map f(z)=z2+c. The triangle towards the top has vertices at the three points 0, c, and c2+c.
Credit: Evelyn Lamb, using the Julia Set Generator by Mark McClure
The Douady rabbit is far from the only fractal to have this kind of behavior, though. I found a fun Mandelbrot/Julia set explorer page by Mark McClure where you can look around and see where this type of behavior occurs. (Be careful, though. The page is quite a rabbit hole!) There you can click around in the Mandelbrot set to find your favorite Julia sets and then see how they change as you move around in the Mandelbrot set. And then once you find a Julia set you like, you can click within it to see how points inside hop around. When you click anywhere near the point c that defines the Douady rabbit, you’ll see a similar-looking fractal, and you’ll see similar triangles of fixed points. The Douady rabbit is just the special one that has 0 as one of the fixed points. McClure's interactive basins of attraction page also features the Douady rabbit.
If the Douady rabbit is not enough for you, there are a few other bunniculous Julia sets to choose from. The “corabbit” is a reversed image of the rabbit, created by changing the parameter c to -0.12256-0.74486i. The “fat rabbit” (or as I like to call it, chubby bunny) corresponds to a nearby c, approximately -.0125+.655i. Perhaps you’d prefer another beautiful set Holly Krieger shared on Twitter a few months ago: “a skinny rabbit made out of fat corabbits,” as she describes it. I even found a paper about “twisted rabbits” that are related to the Douady rabbit. (The paper is quite technical, but it has some pretty pictures.)
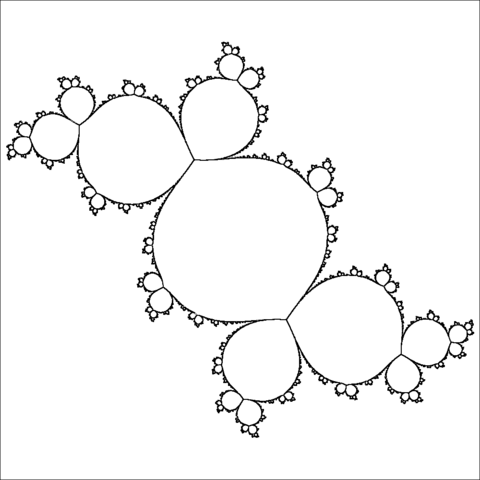
The fat rabbit, or chubby bunny, is the Julia set for the function f(z)=z2+-0.12565651+0.65720i. Credit: Adam Majewski Wikimedia(CC BY-SA 3.0)
If you’d prefer your rabbit fractal to actually bear a resemblance to a rabbit, Kathryn Lindsey wrote a paper detailing how to approximate even a very complicated picture with the Julia set of a complex function. I wrote about that work a few years ago. She and coauthor Malik Younsi recently published a paper expanding on that work.
With all these possibilities, hare’s hopping you can find some fractal bunnies that strike your fancy.
Read about more of my favorite spaces: The Cantor Set Fat Cantor Sets The Topologist’s Sine Curve Cantor's Leaky Tent The Infinite Earring The Line with Two Origins The House with Two Rooms The Fano Plane The Torus The Three-Torus The Möbius Strip The Long Line Space-Filling Curves The Wallis Sieve Two Tori Glued along a Slit The Empty Set The Menger Sponge The Connected Sum of Four Hopf Links Borromean Rings The Sierpinski Triangle Lexicographic Ordering on the Unit Square The SNCF Metric The Mandelbrot Set Fatou's Pancake The Pseudosphere