This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
Consider the square.
.png?w=350)
Credit: Evelyn Lamb
What a nice square. So solid and predictable. Just sitting there on the x-axis minding its own business, blissfully unaware of the weird math we’re about to throw at it.
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
That weird math starts with something called lexicographic ordering. It seems pretty innocuous at first. We’re going to declare that some points in the unit square are “less” than others, the way the number 1 is less than the number 2. In this case, the point (a,b) in the square is less than the point (c,d) if one of two conditions are met: either the first coordinate a is less than c, or a equals c and the second coordinate b is less than d. (We call this the lexicographic ordering because it’s similar to the way we alphabetize words.)
If we pick two points in the unit square, we can always declare one of them to be less than the other one. For example, the point (1/3,1/2) is less than (1/2,1/3) because its x value (1/3) is less than 1/2. It’s also less than (1/3,3/4) because their x values are the same and its y value is less. So far, so good.
Now things are going to get weird: we’re going to use that ordering to define open sets on the unit square. In topology, open sets are destiny. They form the basis for our understanding of a mathematical space. The usual way of dealing with the number line, for instance, relies on using open sets that are intervals, like the span (0,1) containing everything greater than 0 and less than 1. For the unit square with lexicographic ordering, we also build open sets by looking at everything strictly between two endpoints.
There are two basic types of open sets in the lexicographic ordering. The plain vanilla ones happen when both endpoints have the same x-coordinate. For example, (1/3,1/2) and (1/3,3/4). In that case, the open set is just the vertical interval between the two points.
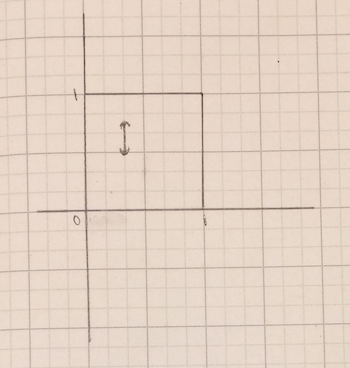
Credit: Evelyn Lamb
If they have different x-coordinates, things get more exciting. The open set with endpoints (1/3,1/2) and (1/2,1/3) has this vertical band between the two points.
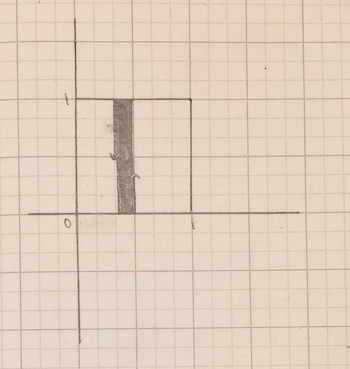
Credit: Evelyn Lamb
As soon as we get “beyond” the top or bottom of the square, the open set automatically gains a vertical band. It might be incredibly narrow, but it will always be there. That’s because there’s no “next” real number in the interval [0,1]. There isn’t a smallest number greater than 1/3 that would let us just go up to the top and then wrap around to the bottom and start again.
That leads to some weirdness: you can have open sets that are less than one unit long and open sets that are infinitely long, but you can’t have anything in between. There are no open sets that are three units long. All of the open sets that stay in one vertical line are finite in length, but the ones that wrap around are infinitely long. This rather inconveniently means that “you can’t get there from here” in this space. (Mathematicians would say the space is not path connected.) If you wanted to walk from the point (1/3,1/2) to (1/2,1/3), you can't find a path to get you from one point to another. They’re infinitely far away from each other from the point of view of this ordering and the topology we get from it. (Mathematicians would say the space is not path connected.)
When I first heard about the unit square with lexicographical ordering, it reminded me of the long line, a space I wrote about in February. The cheeky way to describe the long line is by saying it’s just like the regular number line, but longer. The more complicated way of describing it is by comparing it to the normal number line. The regular number line can be thought of as having one unit of length for every whole number. The long line has one unit of length for every real number. (At least that’s the case if you believe the continuum hypothesis. But you’ll have to read the post to get into that.)
Even though they’re presented very differently, it took me a little while to convince myself that the long line and unit square with lexicographic ordering weren’t really the same space in different outfits. (When I flipped through my copy of Counterexamples in Topology I felt vindicated when I saw that they have an awful lot of properties in common.)
Both spaces are in some sense a conglomeration of infinitely many (in fact, uncountably many) copies of a unit interval. But there are a few differences. One of them is path connectedness. We just saw that the unit square with lexicographic order is not path-connected, but the long line is. The definition of the long line gives you an ordering for free, so you don’t run into the same problem that kept the unit square from being path connected.
If that sounds weird to you, it’s because it is. Orderings aren't cheap. Or at least well-orderings, where you can always say what the “smallest” number in a set is, aren’t cheap. We are good at well-ordering small-ish infinite sets, like the whole numbers, but we’ve never figured out a way to well-order a set as infinite as the real numbers. We can say that 1/3 is less than 1/2, but we can’t say what the smallest number greater than 1/3 is. But when we define the long line, we get to start with an ordered uncountable set. It’s much more convenient, and it means we always know what comes next. So for any two points on the long line, we can figure out how far apart they are, and we can get between two points by traversing a finite, though perhaps very long, distance.
If contemplating the mysteries of the lexicographic ordering on the unit square and the long line haven’t exhausted you yet, it’s fun to think about what would change about the unit square with lexicographic order if you changed it from a closed unit square to an open one by deciding that the top and bottom and two sides are no longer part of the space. Does it get more or less weird?
Read about more of my favorite spaces: The Cantor Set Fat Cantor Sets The Topologist’s Sine Curve Cantor's Leaky Tent The Infinite Earring The Line with Two Origins The House with Two Rooms The Fano Plane The Torus The Three-Torus The Möbius Strip The Long Line Space-Filling Curves The Wallis Sieve Two Tori Glued along a Slit The Empty Set The Menger Sponge The Connected Sum of Four Hopf Links Borromean Rings The Sierpinski Triangle
