This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
One of the highlights of my teaching career was the day a student walked into my classroom with a pseudosphere. It was a beautiful pseudosphere, handmade out of wood on a lathe. (He wrote about making it on the class blog.) We had been talking about the pseudosphere in our math history unit about the development of non-Euclidean geometry, but I never dreamed that a student would replace my terrible sketches on the blackboard with a hefty model, much less one as handsome as this one.
The pseudosphere is a surface with constant negative curvature. Curvature is a bit tricky to define rigorously, but it’s not too hard to get a feel for what it means. It’s a measure of how far a portion of a surface is from being flat. Curvature can be positive, negative, or zero. It’s easiest to think about what these mean if you imagine sitting on the surface. If you sit on a large ball, the surface of the ball curves away from you in every direction. That’s positive curvature. If you sit on a saddle, the saddle curves away from you in the direction your legs are hanging down and up towards you the other direction. That’s negative curvature. A surface with zero curvature is flat.
The three types of curvature correspond to three basic types of two-dimensional geometry: positive curvature corresponds to spherical or elliptic geometry. That’s the kind of geometry we do when we’re trying to navigate over large distances on the Earth. Zero curvature is familiar Euclidean geometry, and negative curvature is hyperbolic geometry. Though some mathematicians came close to discovering it a few times, that last option, hyperbolic geometry, was not recognized as a viable system until the 1830s, when Nikolai Lobachevsky and János Bolyai discovered that it was just as consistent as Euclidean geometry.
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
Johann Lambert, an 18th-century Swiss mathematician, came tantalizingly close to discovering (or inventing) hyperbolic geometry a few decades before Bolyai and Lobachevsky. In a post I wrote two years ago, I shared the following quote from one of his papers. The second and third hypotheses he refers to basically amount to whether the infamous Euclidean parallel postulate is violated in the spherical direction, which yields triangles with an interior angle sum greater than 180 degrees, or in the hyperbolic direction, which yields triangles with an interior angle sum less than 180 degrees.
To come back to the third hypothesis. As we have just seen, under this hypothesis the sum of the three angles in every triangle is less than 180 degrees, or two right angles. But the difference up to 180 degrees increases like the area of the triangle...
I will add just the following remark. Entirely analogous theorems hold under the second hypothesis except that under it the angle sum in every triangle is greater than 180 degrees. The excess is always proportional to the area of the triangle.
I think it remarkable that the second hypothesis holds if instead of a plane triangle we take a spherical one, for its angle sum is greater than 180 degrees and the excess is also proportional to the area of the triangle….
From this I should almost conclude that the third hypothesis holds on some imaginary sphere.
The pseudosphere is that imaginary sphere.
Well, sort of. Lambert was referring to the area formula for spherical triangles, which states that if the radius of a sphere is some number R and the angles of a triangle on that sphere are a, b, and c, then the area of that triangle is (a+b+c-π)R2. Lambert discovered that if you assume what he called the “third hypothesis” (and mathematicians now would think of as the hyperbolic version of the parallel postulate) the area of a triangle with angles a, b, and c would be (π-a-b-c)R2, where R was a constant. So he had noticed that if we plugged an imaginary number into the formula for the area of the sphere, replacing R with iR, where i2=-1, we would get exactly the formula for triangle area that he had discovered assuming the third hypothesis.
The pseudosphere is not defined by equations that are equivalent to replacing the radius of a sphere with an imaginary number. But I still believe Lambert’s remarks foreshadowed this lovely figure. The pseudosphere’s name comes from the fact that it shares an important feature of the sphere: it has constant curvature. There are other objects, like eggs, with positive curvature everywhere, but a sphere is the only object with constant positive curvature. Every point of the sphere looks the same from the standpoint of curvature. Likewise, a pseudosphere, except for at the sharp cusp in the middle, has constant negative curvature. That makes it a natural habitat for hyperbolic geometry just like a sphere is the natural habitat for spherical geometry. Unlike in the case of positive curvature, the pseudosphere is not unique in this property. There are many, many surfaces with constant negative curvature that are not equivalent to one another in other ways.
To make a pseudosphere, you take a tractrix, a curve in the plane first studied by Louvre architect Claude Perrault (who unfortunately didn’t see fit to use it in the Louvre) in 1670, and rotate it around an axis.
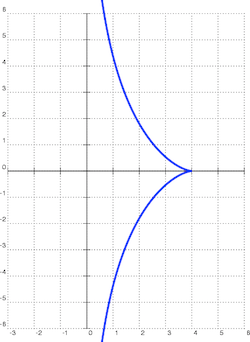
A tractrix. Credit: Pedro Sánchez (CC BY-SA 3.0)
In 1868, Italian mathematician Eugenio Beltrami published a paper about how the pseudosphere could be used to realize the non-Euclidean geometry Lobachevsky had written about decades earlier.

A pseudosphere made by rotating the tractrix around an axis. Credit: Claudio Rocchini (CC BY-SA 3.0)
At the top of this post, I have given the pseudosphere the Magritte treatment by pointing out “Ceci n’est pas une pseudosphère.” The treachery of this pseudosphere is not the treachery of Magritte’s famous non-pipe. It isn’t just that this pseudosphere is pixels on a screen instead of the real, three-dimensional object. No, this wooden model, as gorgeous as it is, is not a pseudosphere either. Aside from whatever small errors were introduced by working with real materials in the real world, the tractrix is an infinite curve, and the pseudosphere therefore continues forever in both directions. Mathematical objects are not the same as real-world objects, and I could append this disclaimer onto any picture of a mathematical object I include in a post. But I think it looks especially classy accompanying this particular mathematical model.
Read about more of my favorite spaces: The Cantor Set Fat Cantor Sets The Topologist’s Sine Curve Cantor's Leaky Tent The Infinite Earring The Line with Two Origins The House with Two Rooms The Fano Plane The Torus The Three-Torus The Möbius Strip The Long Line Space-Filling Curves The Wallis Sieve Two Tori Glued along a Slit The Empty Set The Menger Sponge The Connected Sum of Four Hopf Links Borromean Rings The Sierpinski Triangle Lexicographic Ordering on the Unit Square The SNCF Metric The Mandelbrot Set Fatou's Pancake
