This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
Last week Aubrey de Grey, a biologist who works for the anti-aging research company Sens, reported that he had made the first breakthrough in about 60 years on a problem called the Hadwiger-Nelson problem, or the problem of finding the chromatic number of the plane.
The chromatic number of the plane is the minimum number of colors required to color all the points in the plane so that no two points that are exactly one unit apart have the same color. Since around the time the problem was posed, mathematicians have known that the number is between four and seven. De Grey’s recent paper shows that at least five colors are required, raising the lower bound. I wrote about the problem and this recent progress on it for Quanta Magazine.
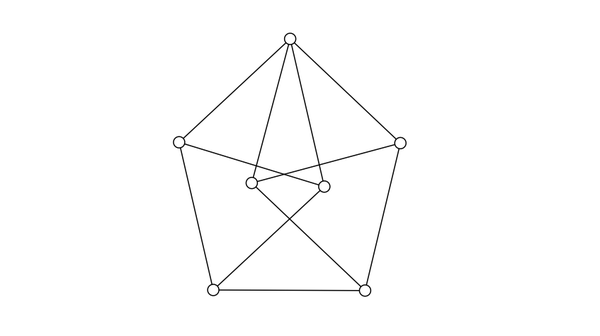
De Grey showed that the chromatic number of the plane must be at least five by finding a graph with unit-length edges, or a unit-distance graph, that requires five colors. To do that, he started with a little graph called the Moser spindle.
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
The Moser spindle has seven points that can be placed so that its 11 edges all have the same length, making it a unit-distance graph. Four colors are required to ensure that no two edge of the Moser spindle connects two points that are the same color, making four a lower bound for the Hadwiger-Nelson problem. The name Moser comes from Leo and William Moser, brothers who were also mathematicians and wrote about the chromatic number in the plane in 1961.
To find his initial non-four-colorable graph, de Grey decided to try assembling graphs with a lot of edges and Moser spindles to see if he could eventually put enough constraints on colorings that no four-coloring could be found. And it worked! The Moser spindle—and hefty doses of ingenuity and good luck—helped him find a non-four-colorable graph.
But I don’t like the Moser spindle just because it is an elegant, useful graph for the purposes of the Hadwiger-Nelson problem. It is also an example that can be used in looking at the four-color theorem, another problem related to graph coloring.
The four-color theorem states that any map on the plane or globe can be colored so that no two countries that share a border are the same color. (Though the problem was stated in the language of cartography, cartographers let out a collective yawn. They don’t generally constrain themselves quite that much when coloring maps and were not particularly interested in the theoretical mathematical constraints on coloring.) In the language of graph theory, the four-color theorem says that the vertices of every planar graph can be colored using four colors so that no two adjacent vertices are the same color.
At first glance, you might wonder why the Hadwiger-Nelson problem isn’t the same as, or even easier than, the four-color theorem. After all, both questions concern graphs in the plane. Confusingly enough, there are non-planar graphs in the plane. A planar graph is not any old graph you can draw in the plane but a graph you can draw in the plane so that the edges don’t cross.
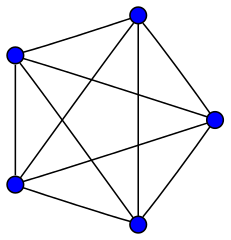
K5, or the complete graph on 5 vertices, is a non-planar graph. Can you convince yourself there is no way to wiggle the edges around in the plane so they don't cross? Credit: Koko90 Wikimedia (CC BY-SA 3.0)
The Moser spindle is also a planar graph, so it can also be used to demonstrate the fact that four colors are necessary for coloring planar graphs. Now I’m being deliberately cheeky. The picture of the Moser spindle at the top of this post is not planar. There are four places where edges cross, and you can’t uncross them while preserving the edge lengths. The Moser spindle, therefore, is both a unit-distance graph and a planar graph, but not at the same time! I think that’s an excellent mathematical joke. (Incidentally, a graph that is both unit-distance and planar is called a matchstick graph because you could assemble it on a table using matches.)
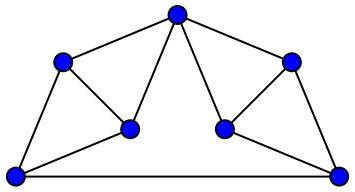
The Moser spindle as a planar graph. The edges no longer cross, but one of them is now much longer than the others. Credit: David Eppstein Wikimedia (CC0 1.0)
Whenever I hear the word spindle, the Schubert song “Gretchen am Spinnrade” (Gretchen at the Spinning-Wheel) starts playing in my head. I couldn’t think of a cute way to work the song into a post about the Moser spindle, but that doesn’t mean you should be deprived of the pleasure of listening to the inimitable Jessye Norman singing the song.
Read about more of my favorite spaces: The Cantor Set Fat Cantor Sets The Topologist’s Sine Curve Cantor's Leaky Tent The Infinite Earring The Line with Two Origins The House with Two Rooms The Fano Plane The Torus The Three-Torus The Möbius Strip The Long Line Space-Filling Curves The Wallis Sieve Two Tori Glued along a Slit The Empty Set The Menger Sponge The Connected Sum of Four Hopf Links Borromean Rings The Sierpinski Triangle Lexicographic Ordering on the Unit Square The SNCF Metric The Mandelbrot Set Fatou's Pancake The Pseudosphere The Douady Rabbit The Poincaré Homology Sphere The Kovalevskaya Top A 6-Holed Torus The Real Projective Plane The 1-Dimensional Sphere The Loch Ness Monster The Koch Snowflake The Bicylinder The Catenoid SO(3) The pseudo-rhombicuboctahedron