This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
In my last post, I wrote about how to “unfold” a rectangular pool table into a torus, or the surface of a bagel or donut. That post is good background reading for this post. The rectangle is a simple example of unfolding a polygon to get a surface. The fact that its four corners fit together, adding up to a perfect 360°, makes it almost too simple. I wanted to see if I really understood how to unfold a pool table by trying another example.
When Maryam Mirzakhani won the Fields medal in 2014, I was struck by the fact that billiards in a pentagon showed up in videos about both her and fellow Fields medalist Artur Avila’s work (at the 1:20 mark in Quanta’s video about Mirzakhani and the 1:00 mark in their video about Avila). So a few days ago, I decided to unfold a pentagonal billiard table and figure out what surface it made.
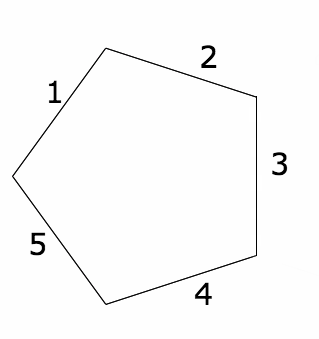
Credit: Evelyn Lamb
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
One way we could unfold the pentagon would be by following a trajectory on the pentagon, like we did with the rectangle. But that’s not really necessary. The important thing about following a point’s trajectory around was that eventually we saw the rectangle rotated and reflected in every possible way that preserves its vertices. So I started with a single pentagon, and I I labeled the edges to help with my bookkeeping. Then I unfolded it across one edge and kept track of which labels went where.
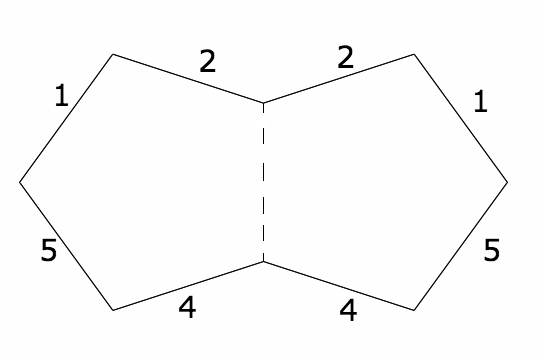
Credit: Evelyn Lamb
Then I repeated it until I had reflected it across every possible edge. My work was a little messier than the computer-generated image above. I worked it out on paper with a bunch of colored pens and pencils. It wasn’t quite as grand a scale as Mirzakhani’s giant paper doodles, but it worked for me. In the end, I had five copies of a double pentagon. (And a little bit of scratch work.)
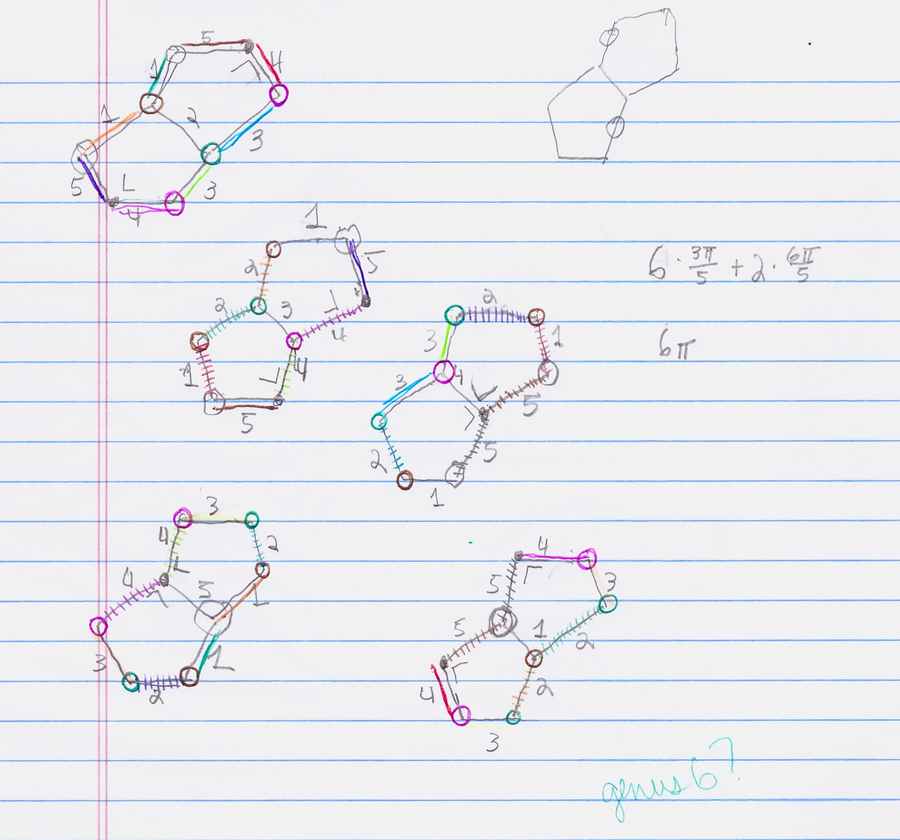
Credit: Evelyn Lamb
It’s pretty easy to visualize the transformation from rectangle into torus. It’s a little less straightforward to take a collection of five eight-sided polygons with a bunch of labeled edges and figure out how many holes the donut will have when you glue all the edges together.
I had kept track of the labels and knew what edges should be glued together, but I needed one more ingredient to figure out the number of holes in my surface: the Gauss-Bonnet theorem.
The Gauss-Bonnet theorem is a magical theorem (not quite my favorite, but close) that relates the curvature of a surface to its topology. It says in part that the total curvature of a many-holed donut is 2π(2-2g), where g is the genus, or number of holes, the surface has. So a donut with just one hole has total curvature 0. There is of course a technical definition of curvature, but it’s OK just to think of it as how bent a surface is. Something flat has 0 curvature, something round like a ball has positive curvature, and something saddle-shaped has negative curvature.
In our case, the polygons we’re unfolding are totally flat. So their faces don’t contribute any curvature to the total. But when we glue them together, we’ll have a few vertices with more than 360° of angle around them. That’s where the curvature lies. When we glued the rectangle together, we got lucky, and the four right angles added up to exactly 360 degrees. In the case of the double pentagon, a little more bookkeeping shows that we have 5 weird points on the surface, each of which has 1080° (6π radians) of angle around it. These points are kind of like parking garages: if you keep driving around one of them, you won’t get back to where you started after 360° of rotation.
For reasons that take longer than this blog post to get into (you’ll just have to take my word for it), the excess angle (that is, the amount above 360 degrees or 2π radians) around each special point contributes to the total curvature of the surface. (It comes in with a negative sign because it makes the surface more negatively curved, like a saddle rather than a ball.) Because the pentagons are flat, all the curvature lives at the vertices, so we can use the Gauss-Bonnet theorem, along with a computation of how much excess angle the surface has, to figure out its genus. The five weird points each contribute 720° (4π radians) of negative curvature to the surface. That’s -20π in total. Plugging it into the Gauss-Bonnet theorem, we see that 2π(2-2g)=20π. We can cancel a few factors on each side to get 2g-2=10, so g=6.
I was really pleased when I finally got the calculation to work out. I was even more excited to consult some billiards references and find out I had done it right! For more information on billiards in polygons, check those references out:
Billiards and Flat Surfaces by Diana Davis (intended for people with less mathematical background)
The Conformal Geometry of Billiards by Laura DeMarco (intended for mathematicians)
There you have it! The pentagon unfolds into a genus six surface, or a six-holed torus. Even though a solitary pentagon seems far removed from a big, complicated surface like that, a particle flowing on either surface would have the same behavior. Analyzing one would explain what happens on the other. I must admit I can't see exactly how the unfolded pentagons would look glued together as a genus 6 surface, but I would be able to do the analysis whether I could visualize it or not. Then again, I might have to get out some fabric and thread and make a companion for Ellie the L-Shaped table, my favorite soft and squishy genus 2 surface.
Read about more of my favorite spaces: The Cantor Set Fat Cantor Sets The Topologist’s Sine Curve Cantor's Leaky Tent The Infinite Earring The Line with Two Origins The House with Two Rooms The Fano Plane The Torus The Three-Torus The Möbius Strip The Long Line Space-Filling Curves The Wallis Sieve Two Tori Glued along a Slit The Empty Set The Menger Sponge The Connected Sum of Four Hopf Links Borromean Rings The Sierpinski Triangle Lexicographic Ordering on the Unit Square The SNCF Metric The Mandelbrot Set Fatou's Pancake The Pseudosphere The Douady Rabbit The Poincaré Homology Sphere The Kovalevskaya Top