This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
Maria Gaetana Agnesi was born May 16, 1718, so her tricentenary was earlier this month. I marked the occasion with an article for Smithsonian. If a modern math enthusiast is aware of Agnesi, it’s most likely through the witch. This curve’s name is the result of a mistranslation made all the more ironic by Agnesi’s fervent religious devotion. That Agnesi, who wrote a groundbreaking tome of a calculus textbook before gradually leaving the world of mathematics to devote herself to pious acts of charity, would be forever saddled with the witch can chafe, but we can probably thank this mistranslation for the fact that she is so well known to those who have taken calculus.
The witch of Agnesi is an excellent example of Stigler’s law of eponymy, which states that no scientific discovery that is named for a person is named for the person who discovered it. Pythagoras was not the first person to know the Pythagorean theorem, Pascal’s triangle was known to Chinese mathematicians centuries before Pascal lived, and the witch of Agnesi was not discovered by Agnesi. Pierre de Fermat (1607-1665) had studied curves of the general form (a2-x2)y=a3, and Guido Grandi had included the curve in a 1703 paper.
Grandi had given the curve the name versiera in the first place, saying he adapted it from the Latin word versoria, which in turn is derived from the word for “turn.” In fact, in some ways 2018 is the 300th birthday not just of Agnesi but of the witch as well; Grandi had discussed the curve in 1703, but he didn’t christen it versiera until 1718.
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
John Colson, the English priest and mathematician who translated Agnesi’s magnum opus into English, translated versiera as avversiera, which means she-devil or witch. Want to hear a grumpy math historian’s take on the mistranslation? (Or at least a math historian’s grumpy take?) Check out this article by C. Truesdell. “Should anyone care to sense my emotions after wasting the time to search out and collect the foregoing, he could well listen to the concerto in D minor for harpsichord by K. P. E. BACH.”
What is the witch? It’s really an unassuming curve when you get down to it, a useful example in her book, one of many. We’ll look at the first appearance of the witch in Agnesi's book Analytical Institutions, as translated by John Colson:
The semicircle ADC, on the diameter AC, being given; out of it a point M is required, such that drawing MB perpendicular to the diameter AC, which shall cut the circle in D, it may be AB.BD::AC.BM. And, because there will be an infinite number of points that will satisfy the Problem, the locus of those points is required.
This setup is just begging for a diagram, and Agnesi supplies one, pictured at the top of this post. (The story goes that she had a printing press moved into her house so she could personally oversee the printing of Analytical Institutions and ensure that the many diagrams she created would be reproduced properly.) It's a little easier to see in this picture.
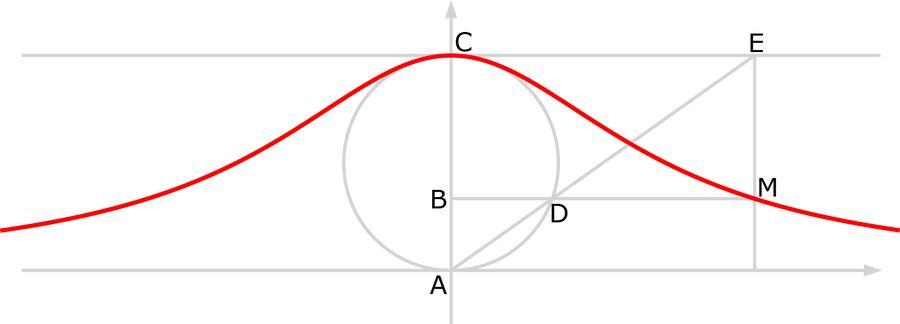
The witch wears red. Credit: Based on zorgit Wikimedia(CC BY-SA 3.0)
Using some basic geometry, Agnesi derives an equation for the curve. In her variables, she arrives at the equation y=a(√(a-x)/(√x). (To us today, her variables are backwards. She used x for a vertical distance and y for a horizontal distance. We would do the opposite.) In a later problem, she showed an equivalent way to describe the curve, which leads to the following gif illustrating the tracing of half of the curve.
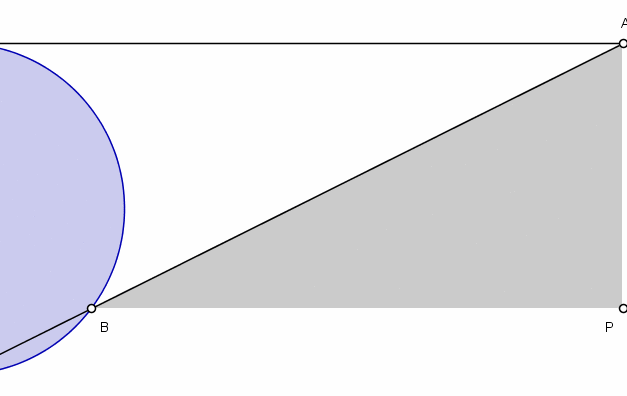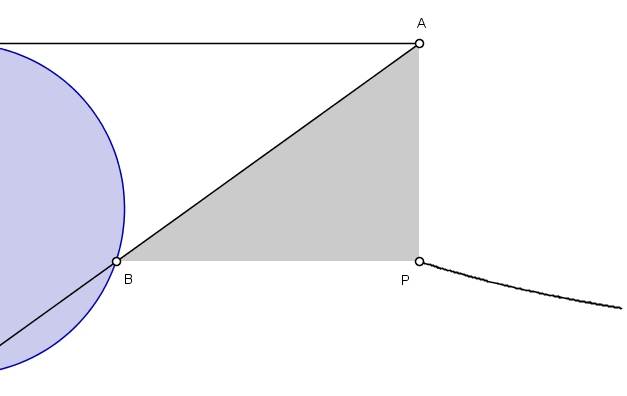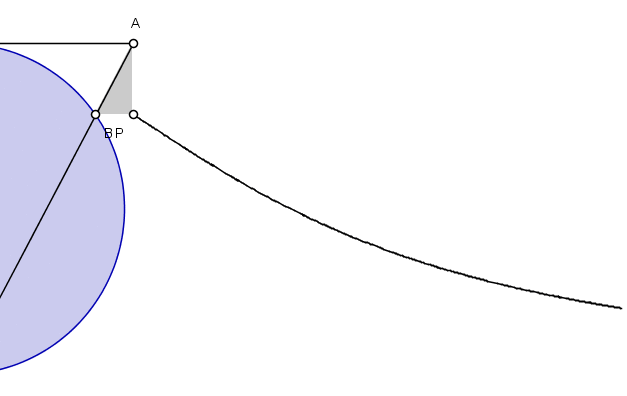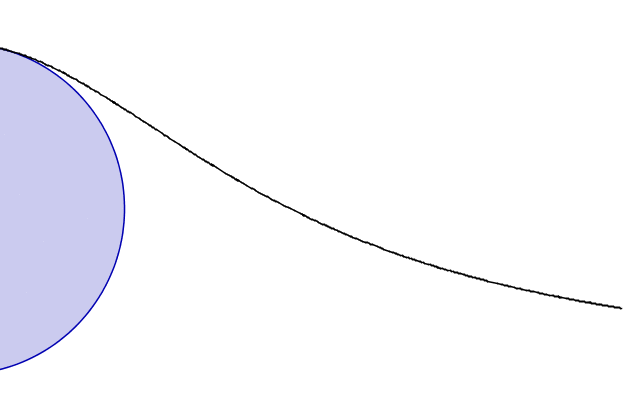
A diagram showing the witch of Agnesi curve. Credit: Merrill Wikimedia
Later still she found the inflection points of the curve. (The curve is curved down like a cap towards the middle and up like a bowl towards the ends. The points where the transition between hat and bowl occurs are the inflection points.)
There’s not too much else to say about the witch. It’s a fine curve, but nothing special. Many calculus students have used it to explore parametric equations, and it’s related to a pathological probability distribution called the Cauchy distribution. If Colson hadn’t let his imagination take a little flight of fancy while he was translating, we wouldn’t have much reason to remember it in particular out of the dozens of examples from Agnesi’s book. It shows what good branding can do for a plucky curve hungry for the limelight.
Want to know more about the witch? Thanks to the magic of the Internet, you can read about the witch in the context of Agnesi’s books for free either in Italian (volume 1, volume 2) or in Colson’s English translation. La versiera appears on pages 382, 392, and 561 of the Italian version. The diagram is figure 135 in the back of the first volume. The witch appears on pages 222 and 229 of book 1 and 79 of book 2 in the English version. You can also explore the curve on the online graphic calculator Desmos.
Read about more of my favorite spaces: The Cantor Set Fat Cantor Sets The Topologist’s Sine Curve Cantor's Leaky Tent The Infinite Earring The Line with Two Origins The House with Two Rooms The Fano Plane The Torus The Three-Torus The Möbius Strip The Long Line Space-Filling Curves The Wallis Sieve Two Tori Glued along a Slit The Empty Set The Menger Sponge The Connected Sum of Four Hopf Links Borromean Rings The Sierpinski Triangle Lexicographic Ordering on the Unit Square The SNCF Metric The Mandelbrot Set Fatou's Pancake The Pseudosphere The Douady Rabbit The Poincaré Homology Sphere The Kovalevskaya Top A 6-Holed Torus The Real Projective Plane The 1-Dimensional Sphere The Loch Ness Monster The Koch Snowflake The Bicylinder The Catenoid SO(3) The pseudo-rhombicuboctahedron The Moser spindle