This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
There are five Platonic solids. Those most highly symmetric solids are the tetrahedron, cube, octahedron, dodecahedron, and icosahedron, the only convex (nothing points in; more like a ball than a star) solids with faces that are all congruent regular polygons. The tetrahedron, octahedron, and icosahedron are built from equilateral triangles (with three, four, or five triangles around each vertex, respectively), the cube from squares, and the dodecahedron from regular pentagons.
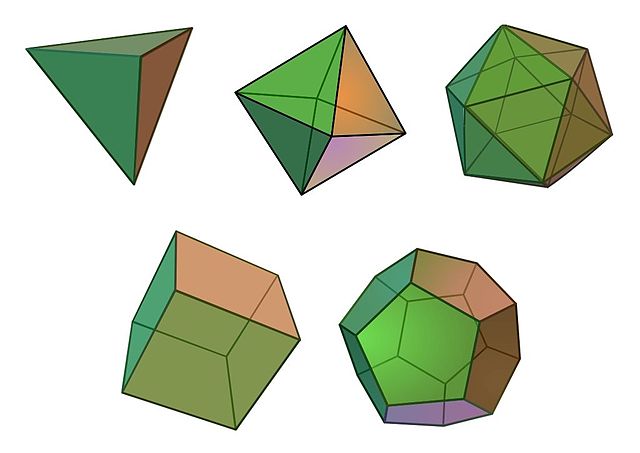
The Platonic solids. Top row: tetrahedron, octahedron, icosahedron. Bottom row: cube, dodecahedron. Credit: Максим Пе Wikimedia (CC BY-SA 4.0)
The Platonic solids are lovely but limited. Once you’ve found them, your mind naturally starts asking what other solids there are that are still pretty regular and symmetric. You might come up with the prisms and anti-prisms next, but to be honest, they can be a bit insipid.
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
Archimedean solids are juicier. Here, the faces are still regular polygons—equilateral triangles, squares, regular pentagons, and so on—but they will mix two or more shapes together. For maximal regularity (what is this, a yogurt commercial?), we still ask that the vertices all look the same. If the shapes around one vertex alternate triangle-pentagon-triangle-pentagon, they all do.
If you sit down with a bunch of polygons, those rules, and a lot of patience, you will find 14 solids that qualify. (You may even find a few extra if you stumble on any near-misses.) But Archimedes’ original list only had 13, and mathematicians have for the most part agreed with his list and use a definition of Archimedean solid that includes only those 13.
The solid that doesn’t belong is called the elongated square gyrobicupola or pseudo-rhombicuboctahedron (solid names are pretty intense).
The pseudo-rhombicuboctahedron, which I will hereinafter call ψρ (“psi-rho”), has 24 vertices with three squares and one equilateral triangle surrounding each vertex. It is a relative of the rhombicuboctahedron, which is an Archimedean solid that also has 24 vertices with three squares and one equilateral triangle around each vertex.
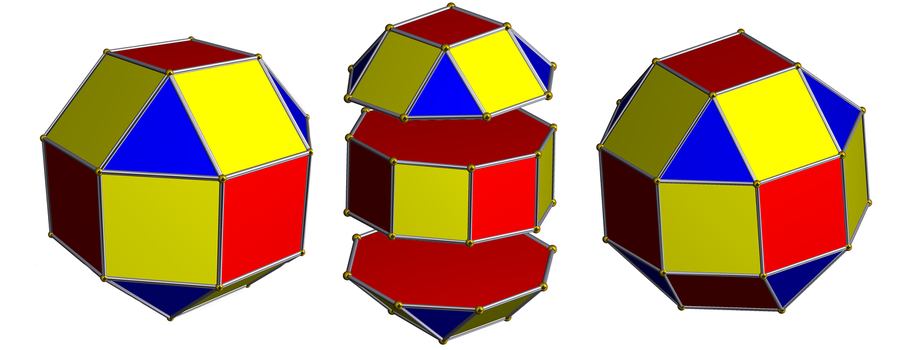
Left: A rhombicuboctahedron. Middle: Dissection showing two cupolae and a band of squares through the middle. Right: A pseudo-rhombicuboctahedron. You can see how to make a rhombicuboctahedron into a pseudo-rhombicuboctahedron by rotating one of the cupolae one eighth of a turn. Credit: Robert Webb's Great Stella software Wikimedia. http://www.software3d.com
To get ψρ from the rhombicuboctahedron, you can detatch the bottom section (which happens to be a shape called the square cupola) and rotate it by an eighth of a full turn.
The rhombicuboctahedron is an Archimedean solid, and ψρ is not. Both are convex solids made from regular polygons, and in both of them, each vertex is surrounded by three squares and a triangle. But the rhombicuboctahedron has a property ψρ does not. You can choose any two vertices on the rhombicuboctahedron and perform a rotation of the object that takes the first vertex to the second. It’s a little harder to visualize than it is for the cube or tetrahedron, but it’s the same idea. If you try the same thing with ψρ, it won’t quite work. It’s not easy to see at first, but the description that helped me the most was thinking of the eight squares in a row along the equator in the above picture as a belt. In the rhombicuboctahedron, there are other similar belts of eight squares going in other directions; in ψρ, there is just one belt. The eighth-twist interrupts the other square belts with triangles.
A ψρ is the only convex polyhedron that has vertices that all look the same but fails to have symmetries of the full object that take each vertex to any other vertex, making it the only convex pseudo-uniform polyhedron. It has one non-convex comrade in this class. I should note that while most mathematicians have agreed that the term Archimedean should refer only to the 13 polyhedra Archimedes listed, the ones that satisfy the global symmetry condition, there are dissenters. Read Branko Grünbaum’s article “An enduring error” to get that perspective.
As I think about ψρ, I find myself succumbing to that all-too-human temptation to anthropomorphize. I imagine ψρ as an outcast. They try to fit in, polishing their faces and sharpening their vertices, trying to sit at a lunch table with their more perfect sibling the rhombicuboctahedron or even the unwieldy truncated tetrahedron. But they just don’t fit in. After yet another humiliating day, they stare at themselves in the mirror, rain trickling down the window behind them to mirror their tears. “Why me?” they ask. “My parents try to console me by talking about the ugly duckling, but there’s no perfect solid for me to grow up into!” Little do they know that the Johnson family has been searching for one polyhedron that went missing at birth. And now we’ve pivoted from Hans Christian Andersen to The Face on the Milk Carton.
But maybe my characterization is wrong. Is ψρ the class clown instead, teasing those who think they have everything figured out? Or perhaps they are the brave visionary who pushes the envelope and teaches us what is possible, the fearless, colorful individual in the gray industrial dystopia who teaches us that it doesn’t have to be like this. In my world, I think ψρ leans more towards the clown. Just when you think you can give a short, simple explanation of what an Archimedean solid is, you have to launch into an description of a technical condition that is only necessary because of this one example! I can just see ψρ snickering, waiting for me to fall in the trap so they can burst out and yell, “Gotcha!”
Read about more of my favorite spaces: The Cantor Set Fat Cantor Sets The Topologist’s Sine Curve Cantor's Leaky Tent The Infinite Earring The Line with Two Origins The House with Two Rooms The Fano Plane The Torus The Three-Torus The Möbius Strip The Long Line Space-Filling Curves The Wallis Sieve Two Tori Glued along a Slit The Empty Set The Menger Sponge The Connected Sum of Four Hopf Links Borromean Rings The Sierpinski Triangle Lexicographic Ordering on the Unit Square The SNCF Metric The Mandelbrot Set Fatou's Pancake The Pseudosphere The Douady Rabbit The Poincaré Homology Sphere The Kovalevskaya Top A 6-Holed Torus The Real Projective Plane The 1-Dimensional Sphere The Loch Ness Monster The Koch Snowflake The Bicylinder The Catenoid SO(3)