This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
It’s somewhat embarrassing that I’ve been writing about my favorite spaces for almost three years and haven’t included any minimal surfaces yet. My advisor Mike Wolf studies minimal surfaces. Although I didn’t end up in that research area, I learned some basics, and the topic came up sometimes when I talked with my academic siblings about their work. So this post is long overdue.
The idea of a minimal surface is that if you take a given boundary curve, there is a surface with least area that has that boundary curve around the edge. (This is called Plateau’s problem after a physicist named Joseph Plateau, not because the surfaces look like plateaus.) Mathematicians, and Plateau himself, particularly love to use soap bubbles as an example. If you start with a wire frame for the bubble, the soap will generally assume a shape that minimizes the area of the film with that wire boundary, as Henry Segerman demonstrates in this video.
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
If you'd like a longer introduction to soap films and minimal surfaces, check out this talk my advisor gave on the topic. Today, the term minimal surface refers to any surface that locally minimizes area. The word locally means that if we look in a small region around any point on the surface, there’s no way to reduce the area in that small region. This means first that we no longer have to have a boundary on the surface. But there are also boundaries that will allow multiple different locally area-minimizing surfaces to span them, as Segerman demonstrates in the video.
The catenoid is one of the first minimal surfaces you’ll encounter in a differential geometry course. If you want to make one out of soap film, you’ll want your boundary to be made of two circles that are parallel to each other and separated by a short distance.

A soap film catenoid. Credit: Blinking Spirit Wikimedia
The catenoid is also the surface of revolution you get by rotating a curve called the catenary around an axis. (The catenary is interesting in and of itself, but that's a story for another blog post.)
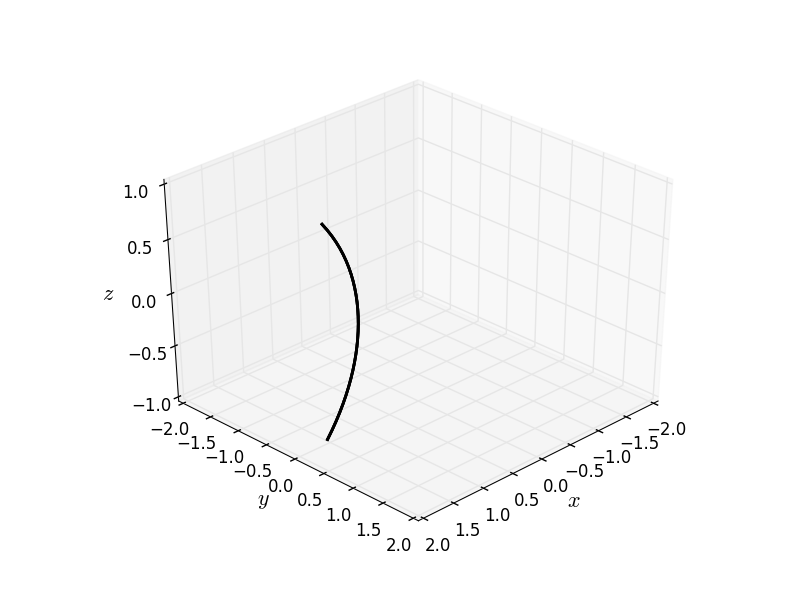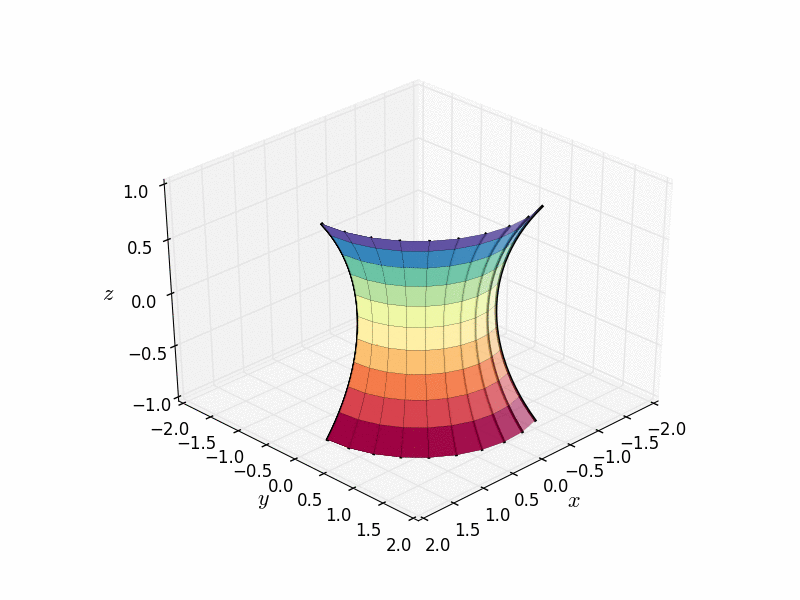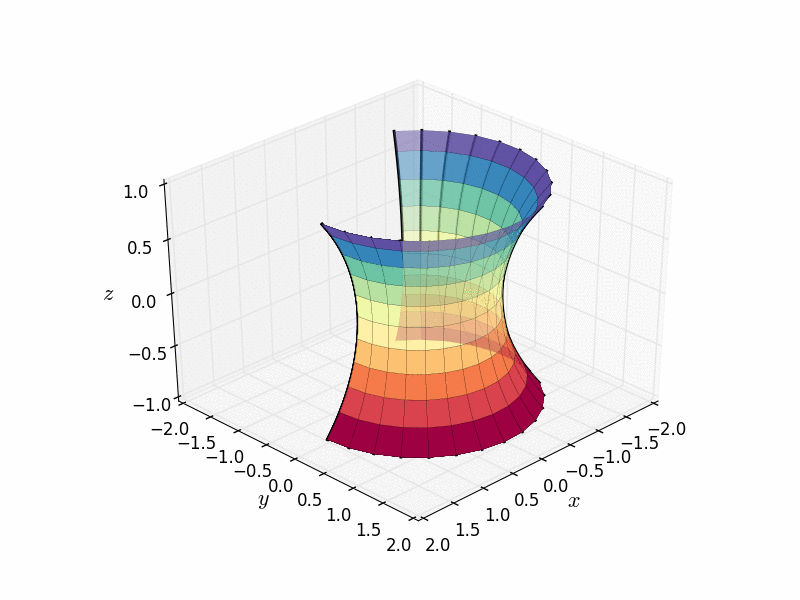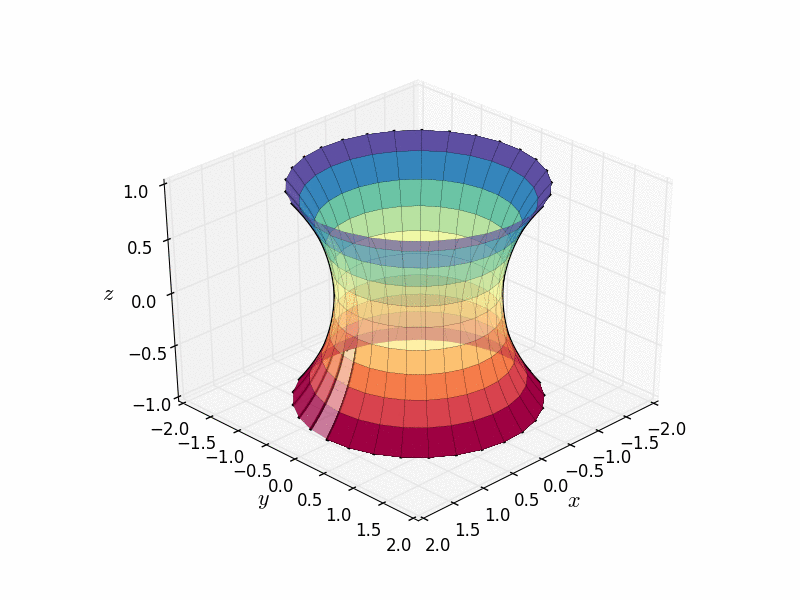
A catenoid created from a catenary curve as a surface of revolution. Credit: Nicoguaro Wikimedia(CC BY 4.0)
You may hear a catenoid called a waisted cylinder because it comes in towards the middle like many humans’ waists. (I like to imagine young catenoids talking about how they were soooo waisted last weekend.)
Examining the catenoid, we can start to notice another characteristic of minimal surfaces. First, we can look at what happens to a soap film catenoid as we move the two boundary circles away from each other, as in this video.
At the beginning, the catenary is just barely bowed in. It’s almost a regular cylinder. But as the circles move, the waist gets more pronounced. (Eventually, there just isn’t enough soap film to sustain the catenoid, so it breaks and collapses to filling the two circles instead, but mathematically we’re going to focus on the time it spends in the catenoid conformation.) Throughout the whole procedure, we can watch how the curvature changes. I wrote about curvature in the show notes for Jeanne Clelland’s episode of My Favorite Theorem. In the catenoid, we’ll look at the curvatures of the curve going between the two boundary circles and the curve going around the waist of the catenoid.
When the curve running between the circles is closer to being flat, the waist curve is closer to being flat. When the circles have moved apart and the curve between them is curvier, the waist gets curvier as well. It happens that these two curves, one bending “up” from the midpoint and one bending “down,” always perfectly balance each other out. That’s not a coincidence that just happens to work for the catenoid. It turns out that a surface with this property, which is called having constant mean curvature zero, is another way to characterize minimal surfaces. In some spots, they can be very curvy and in some spots more gently curved, as long as the curvatures balance out perfectly.
The catenoid itself is a beautifully symmetric, lovely form, but it has another superpower. With just one cut and some careful manipulation, it can transform into (part of) a helicoid, another minimal surface, without stretching or squishing.

The transformation between catenoid and helicoid. Credit: Wickerprints Wikimedia
In 1776, the catenoid and helicoid were the first nontrivial surfaces shown to be minimal. (A flat plane or portion thereof is the trivial example.) In the centuries since, mathematicians have discovered a menagerie of increasingly exotic minimal structures with fancy self-intersections, repeating sections, or holes. But for elegant simplicity, you can't beat the catenoid.
Read about more of my favorite spaces: The Cantor Set Fat Cantor Sets The Topologist’s Sine Curve Cantor's Leaky Tent The Infinite Earring The Line with Two Origins The House with Two Rooms The Fano Plane The Torus The Three-Torus The Möbius Strip The Long Line Space-Filling Curves The Wallis Sieve Two Tori Glued along a Slit The Empty Set The Menger Sponge The Connected Sum of Four Hopf Links Borromean Rings The Sierpinski Triangle Lexicographic Ordering on the Unit Square The SNCF Metric The Mandelbrot Set Fatou's Pancake The Pseudosphere The Douady Rabbit The Poincaré Homology Sphere The Kovalevskaya Top A 6-Holed Torus The Real Projective Plane The 1-Dimensional Sphere The Loch Ness Monster The Koch Snowflake The Bicylinder