This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
In today’s episode of My Favorite Theorem, my cohost Kevin got a chance to talk with University of Colorado at Boulder math professor Jeanne Clelland. They recorded the episode in person at the Metric Geometry and Gerrymandering Group conference at Tufts University last summer, and I could not join them. You can listen to the episode here or at kpknudson.com.
Clelland chose the Gauss-Bonnet theorem as her favorite, and I must say she made a persuasive enough case that I’m seriously considering trading in my uniformization theorem for Gauss-Bonnet. We’ve been using the Gauss-Bonnet theorem as our banner image on our Twitter and Facebook pages, so it was nice of Dr. Clelland to make sure we are not doing any false advertising!
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
The Gauss-Bonnet theorem is truly a marvel. Like my favorite theorem and Emille Davie Lawrence’s favorite theorem, it is about two-dimensional surfaces. There are generalizations, but Dr. Clelland focused on the case of compact two-dimensional surfaces, meaning they are finite and unpunctured, like the glaze of a donut or surface of a pretzel.
The Gauss-Bonnet theorem states that the total curvature of such a surface, or the integral of the curvature over the service, depends only on the number of holes it has, also known as its genus. A sphere has genus 0, a torus or donut genus 1, and so on.
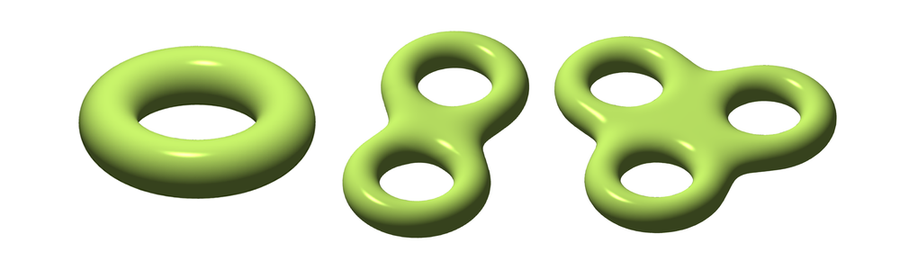
From left to right: pictures of surfaces of genus one, two, and three. Credit: Based on images by Oleg Alexandrov
The curvature of a surface is a way to quantify how much the surface bends. If at a given point, every line on the surface bends in the same direction from a tangent plane, the way they do on a ball, then it has positive curvature at that point. If some lines on the surface bend in one direction and some in another, the way a saddle bends up from front to back and down from side to side, the surface has negative curvature at that point. If the surface doesn’t bend along some line, like the “height” direction of a cylinder, it has zero curvature. Curvature is close to zero when a surface is almost flat and far from zero when it’s very bendy. So a beach ball has lower curvature at any given point than a marble.

From left to right: surfaces with negative, zero, and positive curvature. Credit: Jhausauer Wikimedia
Curvature can vary around a surface, but the Gauss-Bonnet theorem says that it always balances out in a certain way that depends only on its genus. When I was doing research, the surfaces I studied had constant curvature, so Gauss-Bonnet meant I could determine the area of a surface based only on its genus. Dr. Clelland also pointed out how the Gauss-Bonnet theorem is related to the area formula for triangles on a sphere.
Clelland decided to eschew the obvious (but delicious) pairing of donuts or bagels with Gauss-Bonnet and instead suggested a fireworks display and Tchaikovsky’s 1812 Overture. You can listen to the episode to hear why they go so well with the Gauss-Bonnet theorem.
Clelland is the author of the book From Frenet to Cartan: The Method of Moving Frames, an advanced undergraduate- or graduate-level textbook about differential geometry. You can find more information about the mathematicians and theorems featured in this podcast, along with other delightful mathematical treats, at kpknudson.com and here at Roots of Unity. A transcript is available here. You can subscribe to and review the podcast on iTunes and other podcast delivery systems. We love to hear from our listeners, so please drop us a line at myfavoritetheorem@gmail.com. Kevin Knudson’s handle on Twitter is @niveknosdunk, and mine is @evelynjlamb. The show itself also has a Twitter feed: @myfavethm and a Facebook page. Join us next time to learn another fascinating piece of mathematics.
Previously on My Favorite Theorem:
Episode 0: Your hosts' favorite theorems Episode 1: Amie Wilkinson’s favorite theorem Episode 2: Dave Richeson's favorite theorem Episode 3: Emille Davie Lawrence's favorite theorem Episode 4: Jordan Ellenberg's favorite theorem Episode 5: Dusa McDuff's favorite theorem Episode 6: Eriko Hironaka's favorite theorem Episode 7: Henry Fowler's favorite theorem Episode 8: Justin Curry's favorite theorem Episode 9: Ami Radunskaya's favorite theorem Episode 10: Mohamed Omar's favorite theorem
