This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
On this episode of My Favorite Theorem, Kevin Knudson and I were pleased to talk with Emille Davie Lawrence. She’s a math professor at the University of San Francisco who studies low-dimensional topology. You can listen here or at kpknudson.com, which also has a transcript of the episode.
For her favorite theorem, Dr. Lawrence chose the classification of compact surfaces, one of the best theorems from a first topology class. The classification theorem states that all surfaces that satisfy some mild requirements are topologically equivalent to a sphere, a sum of tori, or a sum of projective planes. (It just so happens that I’ve written about both the torus before, and a post on the projective plane is coming soon. It's a delightful non-orientable surface, like a more intense Möbius band.) Topological equivalence allows a lot of leeway. As long as you can deform one shape into another without puncturing or gluing anything, the two shapes are topologically equivalent.
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
The classification theorem for compact surfaces says that as far as topology is concerned, the torus and projective plane form the building blocks of all other surfaces except for the sphere, which is just hanging out by itself. If you’re wondering what it means to take the sum of two surfaces, it’s pretty intuitive. You just cut a little hole in each one and sew the two surfaces together along the holes.

An illustration of the process of taking the connected sum of two surfaces. Credit: Oleg Alexandrov Wikimedia (CC BY-SA 3.0)
If you’ve listened to Episode 0 of My Favorite Theorem, Dr. Lawrence’s favorite theorem might sound familiar. It’s closely related to my personal favorite theorem, the uniformization theorem. They apply to slightly different types of surfaces. The surface classification theorem is for any two-dimensional surface that doesn't have any punctures, but the uniformization theorem only applies to surfaces called Riemann surfaces. The most important difference is that Riemann surfaces must be orientable, so the uniformization theorem doesn't apply to sums of projective planes, which the surface classification theorem has no problem with. Instead of classifying surfaces by topology, the uniformization theorem says that orientable surfaces can have three different types of geometry. It can team up with the surface classification theorem and show that each orientable surface has a natural geometry. A surface with no holes, like a beach ball, naturally admits spherical or elliptic geometry. A surface with one hold naturally admits flat geometry, and a surface with many holes naturally admits hyperbolic geometry.
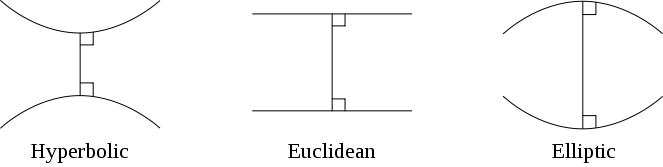
Diagrams of hyperbolic, Euclidean, and elliptic (or spherical) geometry. In hyperbolic geometry, parallel lines move away from each other. In Euclidean geometry, they stay the same distance apart, and in elliptic geometry, there are no nonintersecting lines. Credit: Pbroks13 and Joshuabowman Wikimedia (CC BY-SA 3.0)
Dr. Lawrence decided to go with a classic pairing for her theorem: a donut and a cup of coffee. It refers to a classic math joke: a topologist is the kind of person who can’t tell a donut from a cup of coffee because they are equivalent when you stretch or squish the surfaces, both having one hole.

A demonstration of the topological equivalence of a mug and a donut. Credit: Lucas V. Barbosa Wikimedia
You can find more information about the mathematicians and theorems featured in this podcast, along with other delightful mathematical treats, at kpknudson.com and here at Roots of Unity. A transcript is available here. You can subscribe and review the podcast on iTunes and other podcast delivery systems. We love to hear from our listeners, so please drop us a line at myfavoritetheorem@gmail.com. Kevin Knudson’s handle on Twitter is @niveknosdunk, and mine is @evelynjlamb. The show itself also has a Twitter feed: @myfavethm and a Facebook page. Join us next time to learn another fascinating piece of mathematics.
Previously on My Favorite Theorem:
Episode 0: Your hosts' favorite theorems Episode 1: Amie Wilkinson’s favorite theorem Episode 2: Dave Richeson's favorite theorem
