This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
University of Florida mathematician Kevin Knudson and I are excited to announce our new math podcast: My Favorite Theorem. In each episode, logically enough, we invite a mathematician on to tell us about their favorite theorem. Because the best things in life are better together, we also ask our guests to pair their theorem with, well, anything: wine, beer, coffee, tea, ice cream flavors, cheese, favorite pieces of music, you name it. We hope you’ll enjoy learning the perfect pairings for some beautiful pieces of math.
We’re very excited about the podcast and hope you will listen here, on the site’s page, or wherever you get your podcasts. New episodes will be published approximately every three weeks. We have a great lineup of guests so far and think you’ll enjoy hearing from mathematicians from different mathematical areas, geographic locations, and mathematical careers.
We decided to start things off with an episode featuring just the two of us and our favorite theorems. You can listen right here or on kpknudson.com, which also has a transcript of the episode.
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
So what are our favorite theorems? We recorded this episode a while ago, on March 23, Emmy Noether’s birthday. I almost picked Noether’s Theorem, which is an important theorem in physics. It relates symmetries of physical systems to conservation laws, as this video explains.
But I didn’t choose Noether’s theorem. It’s not really my favorite, and I am just too honest for that. Instead, I chose the uniformization theorem. This is a theorem in topology that states that two-dimensional surfaces can have three basic geometries: spherical (also known as elliptic), Euclidean (also known as flat), and hyperbolic. Spherical geometry, as it sounds, is what you get if you live on the surface of a sphere. The “straight lines” are great circles, like our Equator or lines of longitude, and they all intersect. Euclidean, or flat, geometry, is the classic two-dimensional plane. Parallel lines in the Euclidean plane stay the same distance apart forever. Hyperbolic geometry is the kind of wonderland you’d live in as an aphid on a piece of kale or a tiny sea creature on a coral reef. There, parallel lines move away from each other.
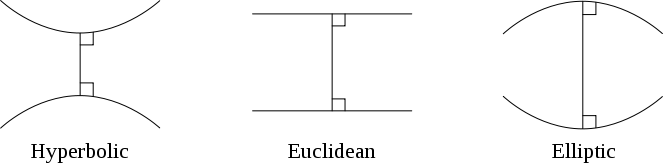
Diagrams of hyperbolic, Euclidean, and elliptic (or spherical) geometry. In hyperbolic geometry, parallel lines move away from each other. In Euclidean geometry, they stay the same distance apart, and in elliptic geometry, there are no nonintersecting lines. Credit: Pbroks13 and Joshuabowman Wikimedia(CC BY-SA 3.0)
Technically, the uniformization theorem is just about surfaces with no holes (in fancier language, simply connected), but the theorem can be used to show that surfaces with holes—donuts, pretzels, and other shapes with many holes—can also be classified into these three types of geometry. (We use the term genus to describe the number of holes a surface has.)

Cold summer treat or edible illustration of the uniformization theorem? Why not both? Credit: Pschemp WIkimedia(CC BY-SA 3.0)
I chose Neapolitan ice cream as the perfect pairing for the uniformization theorem. Two-dimensional geometry comes in three flavors: spherical, Euclidean/flat, and hyperbolic. Neapolitan is the ice cream that combines chocolate, vanilla, and strawberry in the same delightful carton. You’ll have to listen to the episode to find out which geometry goes with which flavor.

My Favorite Theorem cohost Kevin Knudson. Credit: Kevin Knudson
Knudson chose the ham sandwich theorem. If you have two slices of bread and a piece of ham, you can (if you find a knife up to the task) cut all three masses exactly in half with just one cut. This is plausible enough for a conventionally-constructed sandwich, but it’s true even if you are very sloppy with how you place the ham on the bread, or even if you put the bread on a plate and leave the ham in the fridge. There’s some cutting plane that bisects all the masses. If you want to bisect a more complicated sandwich, you can…as long as you make your sandwich with higher-dimensional materials. The number of masses you want to bisect determines the dimension in which your sandwich must exist.
.JPG?w=300)
The perfect beer to enjoy with the ham sandwich theorem. Credit: Kevin Knudson
Sandwiches aren’t fancy, so Knudson chose to pair a beer with his theorem. Specifically, he thinks the 72 Pale Ale from Gainesville’s First Magnitude Brewing is the perfect match.
You can find more information about the mathematicians and theorems featured in this podcast, along with other delightful mathematical treats, at kpknudson.com and here at Roots of Unity. A transcript is available here. You can subscribe and review the podcast on iTunes or wherever you get podcasts. We love to hear from our listeners, so please drop us a line at myfavoritetheorem@gmail.com. Kevin Knudson’s handle on Twitter is @niveknosdunk, and mine is @evelynjlamb. The show itself also has a Twitter feed: @myfavethm and a Facebook page. Join us next time to learn another fascinating piece of mathematics.