This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
In this episode of My Favorite Theorem, my cohost Kevin Knudson and I were excited to talk to Mohamed Omar, a math professor at Harvey Mudd College. You can listen to the episode here or at kpknudson.com.
Dr. Omar’s favorite theorem is Burnside’s Lemma. Mathematicians usually use the word “lemma” for a smaller theorem or one that is used in the proof of a larger theorem, but this lemma is an impressive theorem in its own right. (And as Dr. Omar pointed out, the theorem didn’t even come from a mathematician named Burnside. So if the Burnside part isn’t right, maybe the lemma part isn’t either, and we can promote it to the status of a theorem.)
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
Burnside’s Lemma concerns combinatorics and algebra. Combinatorics is basically counting. It’s a little tougher than using your fingers, though. You might be trying to determine how many full houses are possible in a deck of cards or how many ways you can arrange pieces on a game board. Algebra is generally the study of symmetries and relationships in sets of mathematical objects. So Burnside’s lemma addresses how the symmetry of an object affects its combinatorics.
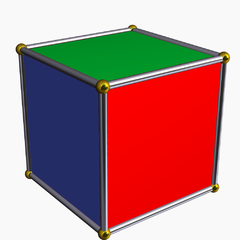
A cube with faces colored red, green, and blue. Burnside's Lemma can help you count how many fundamentally different ways there are to color the faces. Credit: Stella Software by Robert Webb Wikimedia
All that is a bit abstract, but Dr. Omar gave us a really concrete example to think about. You start with a cube, and you can color each face red, green, or blue. How many different ways can you color it? Using just that information, there are 3 choices of how to color each face and 6 faces, so you get 36 or 729 possible colorings. But things get a little silly if you count that way. A cube with the top face red and all the other faces green is different from a cube with the bottom face red and all the other faces green. But it’s easy to make one of those cubes into the other one just by flipping it over. You probably want to consider those two colorings the same, and any two colorings for which you can pick one up and rotate it around to get the other one.
That’s where Burnside’s Lemma comes in. It allows you to use the set of symmetries of the cube, which forms a structure called a group, to count the possible colorings more accurately. And the lemma isn’t just for cubes and colorings. Any time you’re studying the configurations or conformations of an object with some set of symmetries, even very abstract ones, you can use Burnside’s Lemma to count them. We used some algebraic terminology in the podcast. Here are some links if you'd like to learn more about some of those terms: Group (or here if you prefer your definition in poetry); Orbits and stabilizers; Orbit stabilizer theorem (for someone with a strong math background).
In each episode of the podcast, we ask our guest to pair their theorem with something: food, beverage, music, literature, or any other delight in life. Dr. Omar chose to pair Burnside’s lemma with a chessboard marble cake. You’ll have to listen to the episode to find out why that makes the perfect pairing for Burnside’s Lemma.
You can find Dr. Omar at his website, on Twitter, or in his book Number Theory Toward RSA Cryptography. You can find more information about the mathematicians and theorems featured in this podcast, along with other delightful mathematical treats, at kpknudson.com and here at Roots of Unity. A transcript is available here. You can subscribe to and review the podcast on iTunes and other podcast delivery systems. We love to hear from our listeners, so please drop us a line at myfavoritetheorem@gmail.com. Kevin Knudson’s handle on Twitter is @niveknosdunk, and mine is @evelynjlamb. The show itself also has a Twitter feed: @myfavethm and a Facebook page. Join us next time to learn another fascinating piece of mathematics.
Previously on My Favorite Theorem:
Episode 0: Your hosts' favorite theorems Episode 1: Amie Wilkinson’s favorite theorem Episode 2: Dave Richeson's favorite theorem Episode 3: Emille Davie Lawrence's favorite theorem Episode 4: Jordan Ellenberg's favorite theorem Episode 5: Dusa McDuff's favorite theorem Episode 6: Eriko Hironaka's favorite theorem Episode 7: Henry Fowler's favorite theorem Episode 8: Justin Curry's favorite theorem Episode 9: Ami Radunskaya's favorite theorem
