This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
Have you ever heard of the Baader-Meinhof phenomenon? If not, I’m sure you’ll hear about it a few more times in the near future. It’s the cognitive phenomenon, sometimes called the frequency illusion, that shows up when after first hearing about or noticing something, you’ll suddenly hear about it several times in short succession.
The Loch Ness Monster space Baader-Meinhof’d me recently. I stumbled across a paper with the space right in the title not too long ago, and obviously the whimsical name caught my eye. I decided to write about it, and as I started to work on this post, another mathematician tweeted about it. It’s just two times, but it comes after more than a decade of never encountering it in my life as a mathematician.
You can build a Loch Ness Monster by adding handles to a regular 2-dimensional plane. To create a mathematical handle, you cut two discs out of the plane and glue a cylinder in between them. In addition to being aesthetically pleasing, a handle also makes the plane more portable. (Perhaps a better name for the space would be the Infinite Suitcase or the Pack-and-Plane.) If one handle is nice, why not add a few more? Or even infinitely many more? Some mathematician with an active imagination decided to call this space the Loch Ness Monster for its resemblance to grainy photos of the mythical Scottish beast.
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
I don’t know if there are any legends about Nessie being a shape-shifter, but the mathematical version seems that way to me. Or perhaps I should think of it as wearing costumes. No sooner had I learned about the Loch Ness Monster surface than I learned about some other evocatively-named mathematical spaces: Jacob’s Ladder, the Infinite Jungle Gym, and Infinite Jail Cell Windows.
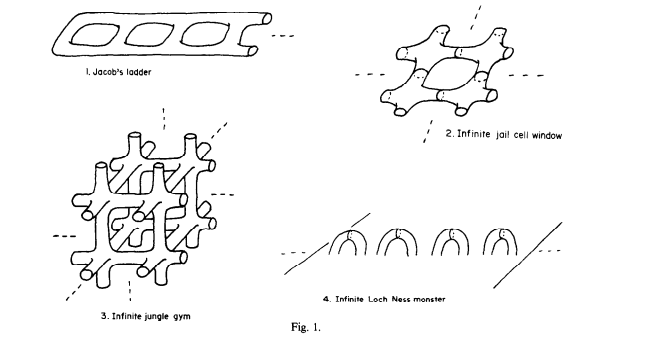
Credit: "Image from Ian Richards' paper "On the Classification of Noncompact Surfaces," Transactions of the AMS Vol. 106, no. 2, 1963.
It turns out that those four spaces are all topologically equivalent! (You should always be suspicious when a mathematician, teacher, or writer says, “It turns out.” They’re probably sweeping some details under the rug, and that phrase turns out to be a pretty big rug. Gosh, I'm doing it again.) Roughly speaking, two spaces are topologically equivalent if you can deform one space into the other by stretching and squishing with no tearing or gluing. There’s a math joke that a topologist can’t tell a donut from a coffee mug because they both have one hole.

A demonstration of the topological equivalence of a mug and a donut. Credit: Lucas V. Barbosa Wikimedia PD-self
Unlike a donut and coffee mug, the topological equivalence of these four spaces is not at all obvious to me. The jungle gym has a three-dimension-ish thing going on where the jail cell windows have a two-ish-ness and Jacob’s ladder is more one-ish.
After my initial shock wore off, I tried to think about how these three very different spaces might be equivalent. I’ve come to the conclusion that this space had two things to tell me: how important the topological notion of end is and the limitations of my finite intuition on infinite spaces.
When I was but a lowly second-year graduate student and had just started reading papers in my advisor’s field, I kept coming across a word that I didn’t understand: end. Obviously I knew the meaning of the word in English, but it was being used mathematically, and I couldn’t figure out its mathematical meaning. It was one of those times where I could almost understand it based on the everyday meaning of the word, but it wasn’t quite right.
In topology, the word end comes up when you start talking about infinite surfaces. Smaller topological surfaces, the surfaces we call compact, have a nice classification: they are all combinations of tori and projective planes. It turns out (there we go again) that these infinite monstrosities also have a classification, this time based on ends.
The basic idea of an end is that it’s a way to travel to infinity on a surface, or, if the idea of going “to infinity” doesn’t resonate for you, it’s a way of walking away from any finite, contained part of the surface. To start with a simple example, the real number line has two ends. If you remove some connected, finite chunk of the number line, there are two separate rays, one going in the positive direction and one going in the negative direction. If you’re on the positive direction side, you can never get to the negative direction side, and vice versa. On the other hand, the 2-dimensional plane has only one end because if you remove a connected chunk of the plane somewhere, you will be able to get from any point in the remaining portion of the plane to any other point.
The classification theorem for non-compact surfaces (pdf) like the Loch Ness Monster says that if certain end behavior of two manifolds is the same, the manifolds are the same. That “behavior” gets a little technical, but basically you need the manifolds to have the same number, genus (number of holes), and orientability of ends.
And that’s how we see that our four infinite surfaces are really the same. They all have just one orientable end with an infinite number of holes in it. To see that, imagine removing some middle portion of any one of the spaces, and imagine making that removed middle part bigger and bigger. With any of the spaces, you can see that the remaining portion is orientable (you’ll never start walking somewhere on the surface and eventually return to the same place accidentally upside down), has an infinite number of holes, and comes in just one piece. In other words, with persistence, you could walk from any part of the remainder to any other part.
It’s a little less than satisfying to have to take a theorem’s word for it that these four spaces are really the same topologically, but I think that’s where I am right now. Even though I can visualize the topological transformations that take any two finite surfaces with the same number of holes to each other, it’s hard for me to believe that these transformations wouldn’t get too wild as we tried to push them farther and farther out on the surface. For now I just have to trust the theorem. I must admit, though, this picture by Spencer Dowdall depicting Nessie as the Jacob's ladder version of the surface helps.
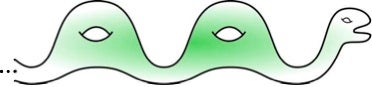
Credit: Spencer Dowdall
Read about more of my favorite spaces: The Cantor Set Fat Cantor Sets The Topologist’s Sine Curve Cantor's Leaky Tent The Infinite Earring The Line with Two Origins The House with Two Rooms The Fano Plane The Torus The Three-Torus The Möbius Strip The Long Line Space-Filling Curves The Wallis Sieve Two Tori Glued along a Slit The Empty Set The Menger Sponge The Connected Sum of Four Hopf Links Borromean Rings The Sierpinski Triangle Lexicographic Ordering on the Unit Square The SNCF Metric The Mandelbrot Set Fatou's Pancake The Pseudosphere The Douady Rabbit The Poincaré Homology Sphere The Kovalevskaya Top A 6-Holed Torus The Real Projective Plane The 1-Dimensional Sphere