The Couple That Studies the Intermediate Value Theorem Together Stays Together

Mathematicians Nikita Nikolaev and Beatriz Navarro Lameda share their favorite theorem and their mathematics-themed wedding

By Evelyn Lamb on February 14, 2019

The Couple That Studies the Intermediate Value Theorem Together Stays Together — Mathematicians Nikita Nikolaev and Beatriz Navarro Lameda stop by the math department on their wedding day. Credit: Dmitri Markine www.dmitrimarkine.com

On this very special Valentine’s Day episode of our podcast My Favorite Theorem, my cohost Kevin Knudson and I talked with Nikita Nikolaev and Beatriz Navarro Lameda, two mathematicians who recently married each other. You can listen to the episode here or at kpknudson.com, where there is also a transcript.

We heard about Nikolaev and Navarro Lameda last month when part of their wedding went a little viral. “Math-shaming” reads the beginning of a Reddit post. “Bride's wedding day math quiz for guests stirs debate online” says another headline. The couple designed a delightfully nerdy and thoughtful mathematical game for their wedding guests. Rest assured, despite what some Redditors seemed to assume, no one left the wedding hungry because they couldn’t solve a math problem. (And as a fact check, despite Yahoo’s headline and the fact that the post was in the “Bridezilla” subreddit, it was the groom, not the bride, whose Facebook post started the whole thing.)

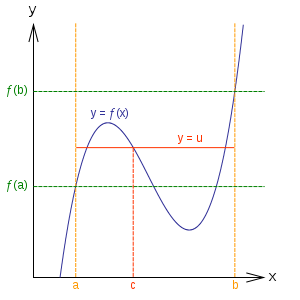
An illustration of the intermediate value theorem. Because the number u is between *f(a)* and *f(b)*, there is some x between a and b such that *f(x)=u*. Credit: Kpengboy *Wikimedia*

The podcast is about theorems, not about weddings, and our guest chose the Intermediate Value Theorem as their joint favorite theorem. After listening to their case, I’m tempted to change my loyalty as well. The Intermediate Value Theorem states that if a continuous function has the value, say, 0 at the point a and 1 at the point b, then somewhere between a and b, it must assume the value 1/2, and somewhere between a and b, it must assume the value 1/3, and 1/π, and every other number between 0 and 1. (Of course, 0 and 1 aren’t special here. Whatever values the function takes on two endpoints, every intermediate value must be attained somewhere between them.)

As Nikolaev and Navarro Lameda describe it, the theorem seems completely obvious when you think about it. How could a continuous function avoid hitting everything between two of its values? But it ends up being extremely powerful. For an introduction to the Intermediate Value Theorem, click here.

As we discussed, it is something of a surprise that the Intermediate Value Theorem does not actually yield a definition of continuity. But there are non-continuous functions that satisfy the property that all intermediate values are attained. One example of such a function is the topologist’s sine curve (more precisely, the function defining the y-value of the topologist’s sine curve. Another even more exotic function, discontinuous at every point, is the Conway base 13 function.

We also talked about the relationship between the Intermediate Value Theorem and the least upper bound property, which you can read about here. Another theorem they mentioned that relies on the Intermediate Value Theorem is Sharkovskii's theorem. One version of that theorem is described as “period three implies chaos.” Sharkovskii’s theorem starts with a re-ordering of the positive whole numbers. Instead of 1,2,3,4,…they go 3,5,7…6,10,14,...,12,20,28,…. In this ordering, if a particular type of mathematical transformation has a period of length n, it has a period of length m for any number m that appears after n on the list. In particular, if it has a period of length 3, it has a period of all other lengths because 3 is the first number on the list.

In each episode of the podcast, we invite our guest (in this case, guests) to pair their theorem with something: food, beverage, art, music, or any other delight in life. You’ll have to listen to the episode to hear their Valentine’s Day-appropriate pairing.

Whether you are newlyweds, oldlyweds, happily single, or anywhere in between, we hope you find some theorem love in your life this Valentine’s Day.

You can find more information about the mathematicians and theorems featured in this podcast, along with other delightful mathematical treats, at kpknudson.com and here at Roots of Unity. A transcript is available here. You can subscribe to and review the podcast on iTunes and other podcast delivery systems. We love to hear from our listeners, so please drop us a line at myfavoritetheorem@gmail.com. Kevin Knudson’s handle on Twitter is @niveknosdunk, and mine is @evelynjlamb. The show itself also has a Twitter feed: @myfavethm and a Facebook page. Join us next time to learn another fascinating piece of mathematics.

Previously on My Favorite Theorem:

The views expressed are those of the author(s) and are not necessarily those of Scientific American.

Rights & Permissions

ABOUT THE AUTHOR(S)

Evelyn Lamb is a freelance math and science writer based in Salt Lake City, Utah. Follow Evelyn Lamb on Twitter

The Couple That Studies the Intermediate Value Theorem Together Stays Together

ABOUT THE AUTHOR(S)

Recent Articles by Evelyn Lamb

The Voices of Black Mathematicians

Pinning Down Uncertainty

ABOUT THE AUTHOR(S)

Recent Articles by Evelyn Lamb

Newsletter

Get smart. Sign up for our email newsletter.

Read More

The Voices of Black Mathematicians

Pinning Down Uncertainty