April 26, 2018

Nalini Joshi's Favorite Theorem

Talking time travel, complex analysis and Burmese food with a mathematician from the University of Sydney

A shot of Nalini Joshi from the shoulders up. She is looking at the camera and smiling. She has long black hair, brown eyes, and brown skin. She is wearing a small brown beaded necklace and a white and blue button-front shirt over a black shirt. — University of Sydney mathematician Nalini Joshi.

Ted Sealey *Wikimedia*(CC BY-SA 4.0)

This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American

On today’s episode of our podcast My Favorite Theorem, my cohost Kevin Knudson and I were happy to talk to Nalini Joshi, an applied mathematician at the University of Sydney. (We were especially amused to be time travelers for this episode. Kevin and I recorded on Thursday afternoon, while Dr. Joshi joined us from Friday morning.) You can listen to the episode here or at kpknudson.com, where there is also a transcript.

Dr. Joshi chose to share Mittag-Leffler’s theorem from complex analysis with us. If you don’t have a background in complex analysis, a little bit of background here might help you understand the big ideas in this episode.

On supporting science journalism

If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.

Complex analysis deals with functions in the complex plane. Points on the complex plane have the form x+iy where x and y are real numbers and i is the square root of -1. But the real power of the complex plane is that by treating points of the plane, which naturally have two coordinates, as single numbers, calculus becomes a lot more powerful.

We can define all the normal calculus stuff in the complex plane as well. For example, the derivative, which is the rate a function is changing at a point, makes sense in the complex plane. But it is much more difficult for a function to be completely differentiable, or analytic, at a point in the complex plane than for a function to have derivatives in a multivariable calculus sense. That’s brushing over a whole bunch of stuff, but the main upshot is that you can think of analytic functions as smooth.

Closely related to functions that are analytic everywhere (also called holomorphic functions) are meromorphic functions. These functions are analytic everywhere except at isolated points called poles, where the function blows up in some kind of controlled way. Dr. Joshi used the vivid image of volcanoes dotting a landscape to describe meromorphic functions. The landscape is smooth and gentle except at the volcanoes.

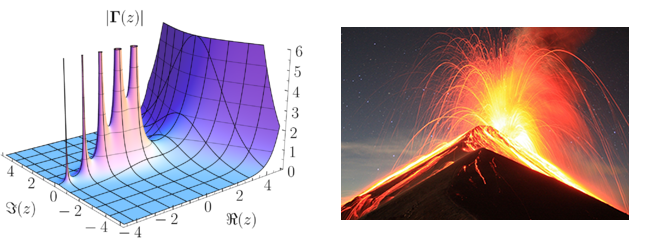
None — Left: graph of a meromorphic function. Right: The Fuego volcano erupts in Guatemala. The two pictures are virtually indistinguishable. Credits: Geek3 *Wikimedia*(CC BY-SA 3.0)*(left)*, Kevin.Sebold *Wikimeda*(CC BY-SA 3.0)*(right)*

Mittag-Leffler’s theorem, named after Swedish mathematician Gösta Mittag-Leffler (1846-1927), concerns complex forensic analysis, a term I just made up. It says that you can basically recreate a meromorphic function if you know the locations of the poles and the behavior, or to use Dr. Joshi’s word, strength of the function around the poles. That information is sufficient to recreate the function, at least up to some wiggle room.

I was surprised that an applied mathematician picked a theorem that seemed to be straight-up complex analysis, a subject I think of as not very applied (though that may just be because of my personal relationship with it). But Dr. Joshi told us how the big idea of Mittag-Leffler’s theorem, the idea of taking local information and translating it into global information, is important to her work building mathematical “toolboxes” that can help people solve problems in the real world. (If you were as curious as I was about her offhand reference to the mathematics of buses of Cuernavaca, Mexico, check out this arxiv paper by Piotr Warchoł.)

In each episode of the podcast, we ask our guest to pair their theorem with food, beverage, art, music, or other delight in life. Dr. Joshi was born in Burma and chose htamin le thoke, a Burmese rice salad with many ingredients mixed in. Like an earlier guest, Ami Radunskaya, she also suggested Steve Reich as appropriate musical accompaniment. You’ll have to listen to the episode to learn why le thoke and Reich are perfect pairings to Mittag-Leffler’s theorem.

You can find Dr. Joshi at her website, on Twitter, or in her book Discrete Systems and Integrability. For more about Mittag-Leffler’s theorem and its history, check out this Historia Mathematica article by Laura E. Turner. You can find more information about the mathematicians and theorems featured in this podcast, along with other delightful mathematical treats, at kpknudson.com and here at Roots of Unity. A transcript is available here. You can subscribe to and review the podcast on iTunes and other podcast delivery systems. We love to hear from our listeners, so please drop us a line at myfavoritetheorem@gmail.com. Kevin Knudson’s handle on Twitter is @niveknosdunk, and mine is @evelynjlamb. The show itself also has a Twitter feed: @myfavethm and a Facebook page. Join us next time to learn another fascinating piece of mathematics.

Previously on My Favorite Theorem: