This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
You trek through the realm of Wisdom. In the distance you see a glimmer. Could it be? Yes, it is the orb you seek! You only have a few more to collect before you have explored the entire surface.
David Madore is the French mathematician who created this and other games played on the hyperbolic plane. Madore’s mazes are some of the many entertaining tools I’ve found to gain an intuition for how hyperbolic geometry works. Others I recommend are Daina Taimina’scrochet projects, which allow you to create touchable models of hyperbolic space, and Malin Christersson’s hyperbolic tiling tool.
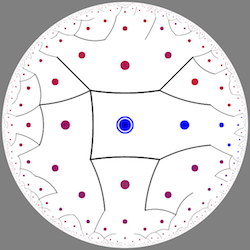
A still from one of David Madore's hyperbolic mazes.
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
Madore has three games available: “toy” and regular versions of a classic maze and a quest for the orbs of wisdom, justice, and other virtues. All three can be played on either the Poincaré disk or the Beltrami-Klein model of the hyperbolic plane. While the games are fun to play whether you care about geometry or not, they also incorporate some sophisticated ideas about hyperbolic surfaces.
To understand the way Madore's mazes work, we'll take a short digression into the standard Euclidean plane. If we walk away from one point on the plane, we will get farther and farther away from that point. (This statement is not quite a tautology; if hypothetically we lived on a sphere, we would eventually start getting closer to the beginning again.) But there is a way to take the infinite plane and make it into a finite space. It's the same technique the makers of wraparound video games such as Asteroids used.
.png?w=300)
An illustration of the way a single-holed torus can be dissected into a square, a two-holed torus into an octagon, and a three-holed torus into a dodecagon. Image from Allen Hatcher's textbook Algebraic Topology.
You start with a square and glue opposite sides together. As you walk off the side of the square, you enter on the opposite side. You can represent this as a torus or donut, as a single square, or as a plane tiled with infinitely many congruent squares. When you walk across the side of one, you walk into the opposite side of the next one. Because these are different ways of representing the same scenario, a path on the Euclidean plane is equivalent to a path around a torus.
Madore’s hyperbolic mazes use the same idea, except instead of a square in the Euclidean plane, we use the hyperbolic plane. If we start with an octagon in the hyperbolic plane, we can glue sides together to get a donut with two holes instead of one. If we start with a dodecagon (twelve sides), we can get a three-holed torus. Surfaces with higher genus can also be represented as polygons in the hyperbolic plane, and that is exactly what Madore does with his hyperbolic mazes. Each one is played on the hyperbolic plane, but the gluings Madore uses mean it's equivalent to playing on a surface with a lot of holes: 4 for the toy version and 8,812 for the full version. Madore includes more detailed explanations of the math he used to create the games at the bottom of the page.
As you play, you can look out for a few interesting aspects of hyperbolic space. First, you can check out the way the hyperbolic tilings seem to change shape as you travel and the board recenters itself. You can also explore the difference between the Poincaré disk and Beltrami-Klein model of hyperbolic space by toggling between the two views. Which one do you like more?
If you prefer topology to geometry, you can examine loops on the surface. One of the most important tools in topology is homotopy, the process of classifying loops in spaces. On a flat plane, any two loops are equivalent in some way: you can drag one onto the other without any trouble. Another way of thinking about this is that any two ways of walking from one specified point to another are the same in some way. On the torus, however, not all loops are equivalent. The loop that circles around the hole in the torus isn’t the same as the loop that you’d get if you put your thumb and forefinger through the hole. Likewise, on surfaces with more holes, there are lots of loops that aren’t the same. One of the challenges Madore issues in the mazes is to go out and back along fundamentally different paths.
You can also use Madore’s mazes to explore one of the defining features of hyperbolic geometry: the fact that straight lines diverge from each other. In the quest game, you can leave “breadcrumbs” behind as you travel. Every once in a while, you will run into past crumbs, but you will find that before you know it, you can’t even see them anymore, even if the trails come very close together for a time.
Can you figure out a good strategy for finding the orbs? Is it better to search one realm exhaustively or just keep walking forward, crossing back and forth through all the realms? How long will it take to find them all? Believe it or not, these questions are related to some topics in ergodic theory and dynamical systems studied by many mathematicians, including Fields Medalists Artur Avila, Elon Lindenstrauss, and Maryam Mirzakhani.
Geometry, topology, and dynamics: not bad for one easy-to-play computer game. Happy exploring!