This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American

A cuddly Klein quartic made with crochet. Image copyright Daina Taimina. Used with permission.
Last week, mathematician and artist Daina Taimina shared her latest creation on Twitter. It's a model of a surface called the Klein quartic. Isn't it cute?
So what is it? The Klein quartic surface is a 2-dimensional object with 3 holes that has a lot of symmetries. In fact, it has as many symmetries as a 3-holed surface can possibly have: 168 that preserve the orientation of the surface and 168 that involve flipping the surface inside out.
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
There are several ways to define the Klein quartic, and Taimina used one that involves sewing 24 heptagons (7-sided shapes) together. It is based on a tiling of the hyperbolic plane by heptagons. OK, but what does that mean?
It's easy to imagine tiling a regular 2-dimensional Euclidean plane by hexagons. We see that all the time, from bathroom tiles to honeycombs. Each angle in a regular hexagon is 120 degrees, and when we stick three of them together at a vertex, we get something with 360 degrees, which is perfectly flat and fits into the plane just right.

These wasps love tiling the plane with regular hexagons! Image: Shardayy, via flickr.
If we use pentagons instead of hexagons, we can still stick three of them together at a point, but instead of ending up with 360 degrees, we only have 324 degrees because each angle of a regular pentagon is 108 degrees. We can't tile the plane with them, but we can stick a bunch of them together and close them up into a very nice surface, the dodecahedron.
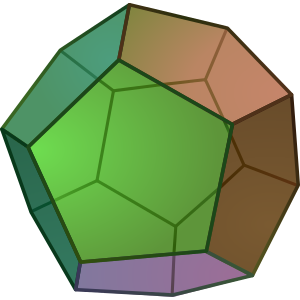
A dodecahedron. Image: DTR, via Wikimedia Commons.
On the other hand, if we use heptagons, instead of an angle deficit, we have an angle surplus. Each interior angle of a regular heptagon is a bit over 128 degrees, so when we put three of them together at a vertex, we get more than 360 degrees. Once again, we can't tile the Euclidean plane with them, but we can tile something called the hyperbolic plane, a mathemagical fairyland where the angles of a triangle don't have to add up to 180 degrees and unicorns are real.*
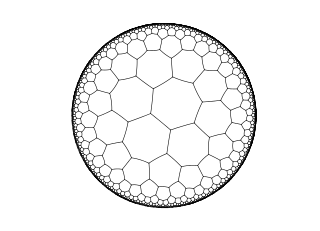
A tiling of the hyperbolic plane by heptagons. Viewed with "hyperbolic eyes," these heptagons are all the same size and have perfectly straight sides. In this picture, some edges are slightly curved to make them "fit" into the Euclidean plane. Image: Theon, via Wikimedia Commons.
Once you've tiled the hyperbolic plane by heptagons, you can glue 24 of them together in a certain way to create a Klein quartic surface, and that is exactly what Taimina did. You can read more details about how she made it on her blog and about some other ways of understanding the surface from John Baez and Greg Egan. The Klein quartic can't be fully realized in 3-dimensional space because we can't make a model of it that has all of the possible symmetries. The white handles on the surface give us an idea of how it would be glued together if Taimina and her crochet model weren't stuck here in boring 3-dimensional Euclidean space with the rest of us.
I've been a fan of Taimina's work for a while. As far as I know, she was the first person to use crochet to create models of the hyperbolic plane and other hyperbolic surfaces. I kind of know how to crochet, and I bought her book Crocheting Adventures with Hyperbolic Planes. When I finally get a chance, I think working on one of the projects from her book will improve both my crochet skills and my understanding of hyperbolic geometry. Taimina has inspired many other mathematicians to create crochet models of hyperbolic space as a teaching tool. I wrote about one of them here. If you're interested in more about Taimina's approach to hyperbolic crochet, check out her website.
*Part of this statement is true.