This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
When I tell people I’m a mathematician, I get a lot of different reactions. Perhaps surprisingly, I mostly get positive responses. Many of them are of the “You go, girl” variety. Some people say, “I’m a [some other profession], but I always liked math” or, "I wish I had taken more math classes." I get a few of the “Wow, you must be smart” comments, which are kind of conversation stoppers. But of course, some people tell me that they hate or are afraid of math.
Here’s a confession: sometimes math scares me too. So for Halloween, I’m going to tell you about some math I find spooky: higher homotopy groups.
Homotopy is a fundamental idea in the mathematical field of topology, the study of shape at its most basic. Two things are homotopic to each other if you can drag one of them onto the other without cutting anything. Homotopy is so fundamental that the first homotopy group of a space is called the fundamental group.
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.

Two homotopic curves and a homotopy taking one to the other. Image: Jim.belk, via Wikimedia Commons.
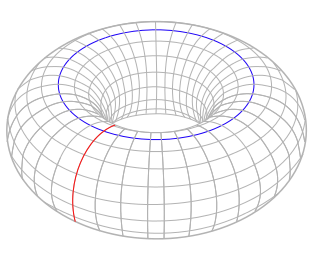
The two highlighted loops on the surface of a donut, colored in red and blue, are not homotopic. Image: YassineMrabet, via Wikimedia Commons. CC BY-SA 3.0
The fundamental group, or π1, has to do with homotopies of loops. I think of the loops as infinitely stretchy rubber bands. You’re allowed to do anything that keeps the rubber band intact and leaves it on the surface or space you’re studying. If you put two rubber bands on a basketball, you can always drag one of them around so it lines up with the other. But if you put a rubber band around the hole of a donut one way, and another rubber band around the hole the other way, you can’t deform one of them into the other without tearing one of them or leaving the surface of the donut. This tells us that a basketball and a donut are not the same: they don’t have the same first homotopy groups. (There was absolutely no way to tell basketballs from donuts before, so it’s quite a relief that we have topology.)
There’s an off-color joke about topologists that is homotopic to, “A topologist is someone who can’t tell a wedding ring from a hole in the ground but can tell it from two holes in the ground.” (If you know the joke, then my version probably made it seem even more off-color.) The joke is about the fundamental group, which basically tells us the number of holes an object has.
Fundamental groups are hard to understand at first. But if you sit around imagining rubber bands on surfaces for a while, π1 starts to make sense. Then you learn about homology groups. They’re a bit like the first homotopy group in that they also measure holes. Sometimes these holes are higher dimensional and therefore harder to visualize, but morally, they're still about holes. The sphere, for example, has no one-dimensional holes—places where you can slide a circle in—but it has a two-dimensional “hole.” It’s a little bit brain-bending, but once again, the intrepid topology student can get comfortable with them.
The first homology group is related to the first homotopy group by something called abelianization. It doesn’t matter too much what abelianization is, but it means the first homology group is a little simpler than the first homotopy group. It also means that the first homotopy group isn’t much more complicated to describe than the first homology group, at least for the types of spaces you see in basic topology classes.
That correspondence between first homology and first homotopy groups can lull the unsuspecting topology student into a false sense of security. For she has heard tell of things called “higher homotopy groups” and assumes that they must share similar relationships to higher homology groups. Higher homology groups aren’t so bad, so higher homotopy groups shouldn’t be either.

There be dragons. Image: Friedrich Johann Justin Bertuch, via Wikimedia Commons. PD-Art.
The nth homotopy group, called πn, of a space relates to how many homotopically distinct maps there are from the n-dimensional sphere to the space. (For our purposes, a circle is the one-dimensional sphere, a basketball is a two-dimensional sphere, and so on.)
The n-dimensional sphere is the simplest n-dimensional manifold, so the higher homotopy groups of the n-dimensional spheres should be a good starting point for understanding higher homotopy groups in general. (She said, blissfully unaware of her peril.) Let’s start with S2, the 2-dimensional sphere. We already saw that π1(S2) is trivial: any loop on the sphere can be deformed into any other loop, so there’s only one class of loops on the sphere. To figure out π2 of S2, we have to think about how many distinct ways we can “wrap” a sphere around itself. If you imagine putting a really stretchy bag around a basketball, you could wrap it around once, or you could wrap it around twice, or three times, or any integer number of times. There would be some weird places where the bag would get scrunched up, but you can kind of imagine that once you wrapped the bag around a few times and sealed it up (this requires the bag to intersect itself; that's not a problem for us), the number of times you wrap the bag around the basketball will tell you something about what kind of map you have. So the second homotopy group of S2 is made up of the integers.

A visualization of some points on the sphere and their fibers in the Hopf fibration. Image: Niles Johnson, via Wikimedia Commons. CC BY-SA 3.0.
What about π3 of S2? This is where my intuition fails. For homology groups, a 2-dimensional manifold can't have any three-dimensional holes in it, so the third homology group and above are all trivial for S2. I want the same thing to be true for homotopy groups. But in 1931, Heinz Hopf discovered the Hopf fibration, a continuous function from the 3-sphere to the 2-sphere, that is not homotopic to the identity map. Hence π3 of S2 is not trivial like I think it should be but is actually generated by the Hopf fibration.
The rest of the higher homotopy groups of S2 get even stranger. π6(S2) is a cyclic group with 12 elements, meaning that there is some map of S6 to S2 where doing it 12 times takes you back to something homotopic to the identity. π14(S2) is generated by one map of order 84 and two maps of order two. I've got goosebumps, and we're just on S2!
There are lots of spooky patterns in the homotopy groups of spheres, so you should check them out if you dare. I can't handle haunted houses, so I'll be over here, playing with my infinitely stretchy rubber bands.