This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American

A demonstration that a tube of toothpaste has a two-dimensional hole. Image: Slipp D. Thomson, via Flickr.
For Halloween, I wrote about a very scary topic: higher homotopy groups. Homotopy is an idea in topology, the field of math concerned with properties of shapes that stay the same no matter how you squish or stretch them, as long as you don't tear them or glue things together. Both homotopy groups and the somewhat related homology groups are different ways to describe the topology of shapes using algebra. In my post, I said that homology detects “holes” of different dimensions. But, as one commenter asked, what do I mean by holes of different dimensions?
Good question! I deliberately used “hole” as a wiggle word because there isn’t a real mathematical definition of hole. But here’s my short answer that is also the reason I’m not an algebraic topologist. If you can put it on a necklace, it has a one-dimensional hole. If you can fill it with toothpaste, it has a two-dimensional hole. For holes of higher dimensions, you’re on your own.
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
That answer isn’t very satisfying. Is there a better way to describe holes? I talked with some of my topologist friends and discovered two things: topologists don't all agree on what a hole is, and it's fun and interesting to think about different interpretations of a word whose mathematical definition isn't completely settled. I think my larger conclusion, in the spirit of the season, is that holes are like Santa Claus: the true meaning is in your heart. So let's look into our hearts and think about what holes are.
The Stanford Encyclopedia of Philosophy has an amusing entry about holes by Robert Casati and Achille Varzi. It starts:
Holes are an interesting case study for ontologists and epistemologists. Naive, untutored descriptions of the world treat holes as objects of reference, on a par with ordinary material objects. (‘There are as many holes in the cheese as there are cookies in the tin.’) And we often appeal to holes to account for causal interactions, or to explain the occurrence of certain events. (‘the water ran out because of the hole in the bucket.’)Hence there is prima facie evidence for the existence of such entities. Yet it might be argued that reference to holes is just a façon de parler, that holes are mere entia representationis, as-if entities, fictions.
Luckily we are mathematicians, not philosophers, so we don’t need to concern ourselves too much with the trivial detail of whether or not holes exist. (Some also take this approach with Santa Claus.)
I have to warn you that this post will end up being a little circular. In some sense, the mathematical definition of an n-dimensional hole "should be" something that causes the n-dimensional homology or homotopy group to have something interesting in it, or to be nontrivial.

A basketball has a hole in it. Image: Public domain, via Wikimedia Commons.
The Mathworld entry on holes has a definition by Eric Weisstein that I like a lot: “A hole in a mathematical object is a topological structure which prevents the object from being continuously shrunk to a point.”
Let’s think about a basketball. Using Weisstein's definition, it definitely has a hole in it because you can’t squish it all the way down to a point without changing its basketballiness.
I like this definition because it’s intuitive, but I think it's a bit dangerous because there are a few different notions of being continuously shrunk to a point that are used in topology, and it’s easy to get them confused. (Trust me. I have lived it.) A circle in the plane can be continuously shrunk to a point,* but intuitively, and in the sense of homotopy and homology, a circle has a hole in it. That notion of shrinking, however, relies on the assumption that the circle is sitting in a 2-dimensional plane, so it’s really telling us something about the topology of the plane, not the topology of the circle. We need our definition not to rely on how something is sitting in space.
The notion of being shrunk down to a point that Weisstein’s definition uses requires us to retain topological equivalence the whole time. We can’t shrink a circle down to a point because we'd end up tearing or squishing something together at the end.
What about defining the dimension of a hole? That's trickier. A tempting definition, and the definition that one of my topologist friends prefers, is that an n-dimensional hole in a manifold is a place where the manifold is "like" the n-sphere. (For our purposes, a one-dimensional sphere is a circle, a two-dimensional sphere is basketball-shaped, and so on. This is because up close, a circle looks like a line, and a sphere looks like a plane.) More rigorously, an n-dimensional hole in an object is something that prevents some map of the n-sphere into the object from being shrunk down into a point without leaving the object. This definition of a hole would mean that we were equating hole-ishness to homotopy. Let's work out some examples.
First, a plane. You can't put it on a necklace or fill it with toothpaste, so it probably doesn't have a hole. Let's check. There are lots of different ways to map a circle into a plane, but all of them can be shrunk down into points while staying on the plane. In other words, there's no obstruction to scooting a rubber band around the plane and shrinking it down as much as we want. So by our working definition, a plane has no one-dimensional holes. That's good because if the plane has a hole, we our definition of a hole is wrong.
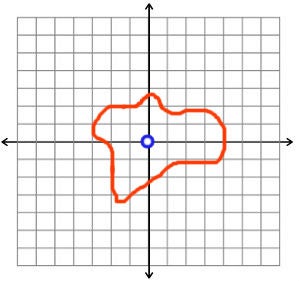
We can tell the punctured plane has a hole because we can't pull the orange loop past the missing point, outlined in blue. Image: Evelyn Lamb.
What about the plane with one point removed? We still can't fill it with toothpaste, but given a really thin chain, we could put it on a necklace, so it should have a one-dimensional hole. How can we see that? If we map a circle into the plane, and the removed point is inside the circle, we have a problem. (Pedants might point out that I haven’t proved that there’s such a thing as an inside and and outside of a map of a circle into a plane, hole or no. You’re right, and you can go write your own blog post about it. The rest of us will just assume that we can find a circle map polite enough to have a clearly defined inside and outside.) We can’t pull or shrink the circle past that point, so we know that the plane minus a point has a one-dimensional hole.
Now back to the basketball we talked about earlier. We know it has a hole. What dimension is its hole? You can't put it on a necklace, but you can fill it with toothpaste, so it's probably two-dimensional. Now to check it. It has no one-dimensional holes because any way you put a rubber band (or circle) on the basketball, you can shrink it down until it's a single point without leaving the surface of the basketball. But it does have a two-dimensional hole because you can’t continuously shrink every map of a two-sphere into the space down to one point without leaving the basketball. (To pick the low-hanging fruit, if your map from a basketball to a basketball is the identity map, where everything stays in the same place, you can't shrink it down to one point.)
So far, the definition of hole we're using seems promising. But in the end, I don't think it's the best one.
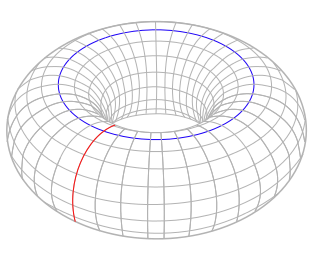
The two highlighted loops on the torus show us the two different one-dimensional holes. Image: YassineMrabet, via Wikimedia Commons.
Let's look at the torus, one of the simplest topological spaces. The torus can be thought of as the glaze of a donut or the surface of an inner tube. We can put it on a necklace or fill it with toothpaste, so it should have one- and two-dimensional holes. Everything is fine for one-dimensional holes: there are basically two main ways a map of a circle can fail to shrink down to a point on a torus. Either it can go around the hole of the donut (the blue circle in the image to the left), or it can be like the circle your fingers would make if you stuck your thumb through the hole of the donut and grasped it with your first finger (the red circle in the image to the left). So the torus has two one-dimensional holes. (You don't find them both with the necklace definition unless you stand inside the torus to wear one of the necklaces.)
Our working definition breaks down when we get to two-dimensional holes. A torus "should" have a two-dimensional hole, but we can't find it using maps of two-spheres. (This isn't obvious, at least to me. You can think about trying to wrap a balloon around an inner tube to get an idea of what's going on.)
Our definition of hole in terms of maps of spheres doesn’t work for the two-dimensional hole in the torus, but I’d really like to say the hole is there. I think the right answer, though it doesn't seem particularly insightful, is to define hole the same way but allow maps of any two-dimensional things instead of just spheres. There is a two-dimensional thing we can map into the torus that can’t be shrunk down to a point while staying on the torus, and it’s the torus itself. So if we know that the torus isn't topologically equivalent to a point, we know that it has a two-dimensional hole. This kind of seems like an "I know it when I see it" definition, and it isn't very helpful in practice. If we don't know much about an object, how will we know which one of the infinitely many two-dimensional surfaces to map into it to test its holiness? But this a version of this notion, defined more precisely, is homology. (For the ambitious, you can read more about it in Allen Hatcher’s free Algebraic Topology textbook. It’s worth noting that Hatcher always uses scare quotes around the word hole because he never defines it.)
There are several ways to define homology, but to me the most intuitive is by taking some fundamental building blocks—vertices, edges, faces, and so on—and looking at how they get stuck together to make the surface. Although it's more subtle than this, homology basically tells you which building blocks of a certain dimension don’t bound higher-dimensional building blocks in your space. This works with the ideas of holes we’ve already seen: the two distinct holes in the torus come from (one-dimensional) circles that don't go around around a (two-dimensional) solid disk in the space. The two-dimensional hole comes from the fact that the torus is only made up of two-dimensional and smaller components, so its two-dimensional components don’t bound any three-dimensional parts of the surface. On the other hand, a solid torus (the whole donut) doesn’t have any two-dimensional parts that aren’t the boundary of three-dimensional parts, so it doesn’t have a two-dimensional hole. (The two-dimensional hole of the donut glaze is now filled with three-dimensional bread. Which is much better than toothpaste.)

A visualization of the Hopf fibration, which demonstrates the surprising fact that a basketball has a three-dimensional hole. Image: Niles Johnson, via Wikimedia Commons.
Mathematicians often refer to homology alone as detecting holes, leaving homotopy—and our earlier working definition of n-dimensional holes—high and dry. One advantage of this definition is that we'll never have a higher-dimensional hole in a lower-dimensional space, a disturbing prospect that is the reason I find higher homotopy groups spooky. If we allow the homotopy-based definition of hole, a basketball has a three-dimensional hole. (So I guess it can be filled with whatever four-dimensional beings use to brush their teeth.) The Hopf fibration, which I also mentioned in my earlier post, is a map from the three-sphere to the two-sphere that can’t shrink down to a point.
So with holes, you get a choice of what definition you like the best. I think I prefer to use the homology definition, but there's something beautiful about the idea that different hole-detectors can detect different holes, so I might try to open my heart—which for simplicity I'm assuming is topologically equivalent to a two-sphere—and let the three-dimensional hole in.
If you made it this far, you deserve a treat. How about a demonstration that a two-sphere filled with watermelon flesh doesn't have a one-dimensional hole?
Thanks to Arunima Ray and two Christopher Davises (Christophers Davis?) for their helpful comments about this post. Anything you didn't like is my fault.
*Recipe for shrinking a circle to a point in the plane: start with a circle of radius 1, and for convenience, set it down at the point (0,0). We'll define a two-variable shrinking map. The first variable will represent a point on the circle, which we’ll identify by angle (measured counterclockwise from the x-axis). The second variable represents time. I can shrink any circle down to a point over the time interval from 0 to 1 with the map F(a,t)=(1-t)a. At any time w strictly between 0 and 1, the image of this map is a circle of radius 1-w. At time 1, we have a “circle” of radius 0, which is also known as a point. Maps like this are used all the time as examples of explicit homotopies between paths.