This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
There's a tired joke about mathematicians (or engineers, or even Finns) that says you can tell a mathematician is an extrovert if they look at your shoes when you talk with them. In truth, mathematicians come in all shapes, sizes, colors, and levels of extroversion, but looking down can be mathematically rewarding. On a trip to Germany to visit some mathematician friends, I was staring at the ground and tripped—almost literally—over a beautiful tiling pattern. Below is a rough transcript of my thoughts while I stared at it.
What a lovely tiling! I don't think I've ever seen one like that before. Or if I have, I haven't noticed it. How many sides do those shapes have? 1, 2, 3, 4, and then they’re all paired. Eight. It’s an octagonal tiling.

The tiling with one octagon outlined in white. Credit: Evelyn Lamb
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
Isn’t it funny how non-convex shapes look so different from convex ones? You can't tile the Euclidean plane with regular octagons. I guess even though these shapes have eight sides each, they’re really just parallelograms or rectangles in disguise. The underlying pattern of this tiling is just a grid.

I put dots at the centers of some of the octagons and then connected them in green to highlight the underlying parallelogram grid for the tiling. Credit: Evelyn Lamb
These octagons have four pairs of parallel sides. That means they’re translation surfaces! I bet my spouse will like that. He’s really into translation surfaces.
Here I interrupt my stream of consciousness recollections to define a translation surface. That's a collection of one or more polygons where the edges come in pairs that are parallel and the same length. You can imagine gluing these pairs together to make the flat polygon into a surface that bends around in space. The torus, or donut, is an example you can make easily at home.

An octagon with edge pairings labeled. Edges that have the same label are the same length and are parallel. Credit: Evelyn Lamb
If you glue opposite sides together on a translation surface, you’ll get some sort of donut, maybe one with multiple holes. I wonder what kind of donut you get with this one. Hey, are there any donut shops around here? No? I'd settle for a pretzel.
It’s hard for me to visualize what would happen if I glued corresponding sides together. Wait, doesn’t a double regular pentagon have eight sides?
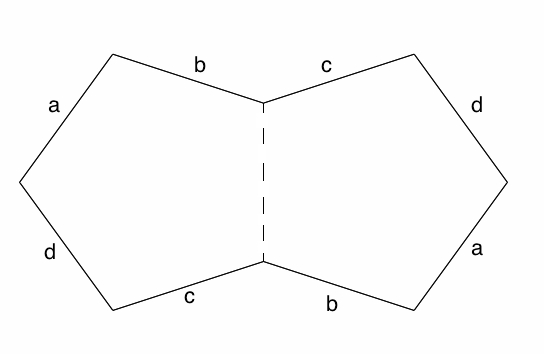
A diagram of the double regular pentagon, two pentagons glued together along the dashed line. Sides labeled with the same letter can be glued together to create a surface. Credit: Evelyn Lamb
Diana Davis’sDance Your PhD video about double pentagons was so cool! I should watch that again!
Cutting Sequences on the Double Pentagon, explained through dance from Diana Davis on Vimeo.
The octagons in the paving stones have the same pattern of parallel sides as the double pentagon, so they must glue up into the same kind of surface as the double pentagon. That's a genus two surface, or a two-holed donut. Seriously, I could really use some pastry right now.
Wait, if the double pentagon is an octagon, there must be some way we could cut the paving stone octagons into pairs of pentagons like in the double pentagon!
.jpg?w=350)
A picture with one of the octagons cut into two pentagons. Credit: Evelyn Lamb
That means this octagonal tiling is also a pentagonal tiling in disguise! I love tiling pentagons! Did I discover a new way to tile the plane with pentagons?!!

The pentagonal tiling is outlined in white. Credit: Evelyn Lamb
That’s pretty unlikely, huh? I bet any tiling pentagons with right angles were discovered a long time ago. I'll have to look it up when I get home.
Indeed, when I looked it up later, I discovered that this pentagon is the same as the first type of tiling pentagon in the chart below. It’s been known for a while.

How can I tile thee? Let me count the ways... Credit: Ed Pegg Jr. Wikimedia(CC BY-SA 4.0)
What are the angles in the pentagons? I don’t have a protractor, but I'd guess something like 90-90-130-60-170.
You might notice that the paving stone octagons don't have exactly the same angles as the one on the top left of the chart. Good eye! There are 15 known types of pentagons that can tile the Euclidean plane, but some of those types have a few degrees of freedom, whole families of pentagons that can tile the plane because they satisfy the same basic rules. The first type of tiling pentagon includes any pentagon with two adjacent angles that add up to 180°.
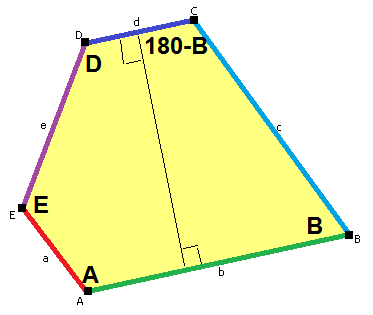
Any pentagon that satisfies the mild criteria above, i.e. that has two adjacent angles that sum to 180°, tiles the plane. Credit: Tomruen Wikimedia(CC BY-SA 4.0)
Staring at this tiling is helping me understand why this kind of pentagon tiles the plane. There are points where the three non-right angles come together and points where the right angles come together with a side of the shape. Any pentagon that has that property must tile the plane!
So this is an octagonal tiling that’s also a pentagonal tiling that’s built on an underlying quadrilateral tiling grid. How cool is that? Does Germany have a lot of tilings like this? I should move to Germany.
If I hadn't noticed the unusual tiles and stopped to admire them for a little while, I never would have taken the time to ponder why this particular type of pentagon tiles the plane and figure it out for myself instead of taking someone else's word for it. Sometimes staring at your feet isn't such a bad thing.
For more #foundmath, follow me on Instagram.
