This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
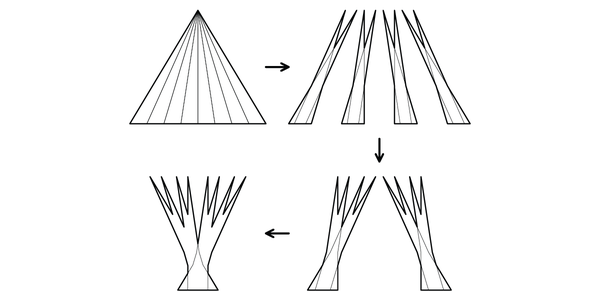
Last year, I wrote about the Kakeya needle problem, a mathematical morsel I turn to for reassurance when I’m worried I might be stuck. The problem asks for the minimal area you need to turn a thin needle around in the plane. Below is one example of a needle turning around in a small area in a plane.
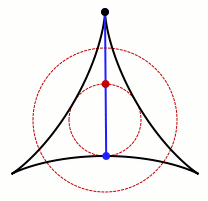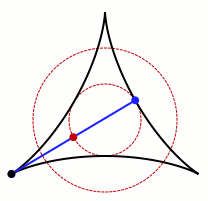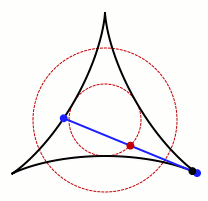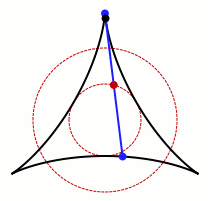
An animation of one set that allows Kakeya's needle to turn around. Credit: Claudio Rocchini Wikimedia (CC BY-SA 3.0)
Surprisingly, a needle can be turned around in a set with arbitrarily small area. This fact was proved by Abram Samoilovitch Besicovitch in 1928. He based the result on his prior work concerning sets in the plane that contain a unit-length segment pointing in every direction. These sets are called Besicovitch sets in his honor.
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
Besicovitch sets can look really cool, so I was excited when I saw a paper about minimal Besicovitch arrangements on the preprint server arxiv.org. When I started reading it, though, I was both disappointed and intrigued. The paper is not about Besicovitch sets in the plane, so I wasn’t going to see a bunch of pretty pictures, but I got to learn about a different version of the Kakeya needle problem. The paper looks at a translation of the Kakeya needle problem to a different mathematical setting, the world of finite fields and planes.
We’re used to doing arithmetic with infinite number fields like the real numbers, but we can also define the basic operations on finite sets of numbers. For example, in modular arithmetic, also called clock arithmetic, you have a modulus—say, 12—and when you add or multiply two numbers, you look at the remainder when you divide by the modulus. The system doesn’t seem as foreign when you think about the fact that five hours after 10:00 is 3:00. We’re used to doing arithmetic with a modulus of 12 or 24 when it comes to telling time. (For technical reasons, for the finite version of the Kakeya needle problem, the modulus needs to be a prime number or a power of a prime number. There are no Kakeya clocks!)
Just as we can think of the two-dimensional plane as the set of all pairs of real numbers, we can consider finite planes made from pairs of members of finite sets. If the modulus is 2, for example, the field just contains the numbers 0 and 1, and the plane is the pairs {(0,0),(0,1),(1,0),(1,1)}. We can look at triples of these numbers as well, and if you’ve been reading Roots of Unity for a while, you might remember a space called the Fano plane. (If not, you can read about it here.) One way of building the Fano plane starts with triples of zeroes and ones, rather than pairs, so in some ways it’s a three-dimensional version of a plane over a finite field. (Read more about that description here.)
Any two points in the standard two-dimensional plane determine a line. The same thing happens in finite planes. The notion of “direction” isn’t as clear-cut in a finite plane as in the standard two-dimensional plane, but people who have studied the finite Kakeya needle problem have defined a Besicovitch set for the finite version to be a set in the plane that contains points from every line in the plane.
Why bother moving Kakeya’s needle to a space as unfamiliar as finite planes? Aside from mathematical curiosity about what happens when you change your assumptions, the question arose due to something called the Kakeya conjecture. While there are Kakeya sets of arbitrarily small area, and Besicovitch sets with zero area (using a standard way of measuring area called Lebesgue measure), the dimension of the set is still 2. Mathematicians have generalized the notion of dimension to encompass sets that have dimensions that aren’t whole numbers, and I sometimes think of having measure zero as a symptom that could indicate that we’re measuring its area in the “wrong” dimension. But for Kakeya, this is not the case. Besicovitch sets in the plane are genuinely two-dimensional. The Kakeya conjecture broadens this idea to higher dimensions: in dimension n, a set with unit length line segments in every direction must have dimension n, even if it has 0 measure in that dimension.
Some mathematicians started looking at the finite plane version as a way to look at the Kakeya conjecture in miniature. Finite and infinite planes have a lot of differences, but if they can make some progress or gain some intuition in finite spaces, they might glean some insight about the more general problem. For more information on the Kakeya conjecture, see this post by Terry Tao or this paper by Zeev Dvir.
I think the finite Kakeya needle problem is a great example of the twisted path mathematics research can take. We start with an interesting problem motivated by natural curiosity about something fairly tangible, generalize the problem into new arenas, discover it’s too hard to solve there, and translate the problem into some other domain, aiming to gain some traction there. The original ideas that motivated the question are changed and obscured, but mathematicians are hopeful that the new, different problem can help them understand the whole picture even better.