This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
This evening’s big excitement was a boat. The two months we’ve lived here, the museum next to our apartment has had a giant boat out in front as part of their exhibit “Aventuriers des mers.” The exhibit closed on Sunday, and today they packed up the boat.
Though I will miss the boat and how easy it made directions (“Walk along the Seine until you see the giant boat. No, not on the water. On the sidewalk.”), the removal of the boat was a source of anticipation and joy. There was a big crane! They picked the boat up with it! It was a marvel of mathematics and engineering. The calculations to make sure the crane and sidewalk could support the weight, the precision with which the workers executed their jobs, and of course the important fact that real life does not commute. The coordinators of the spectacle needed to understand and plan everything in just the right order. (Click here for an article in French about part of its trip to Paris, including a video of part of the journey.)
At the end of all the excitement, the crew had picked up a boat with the crane and put it on a flatbed truck. The truck carrying the boat had to somehow get the boat from the public square/sidewalk where it was sitting onto the roads of Paris.
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.

The boat rests on the truck. Credit: Evelyn Lamb
I looked at the boat and truck and to the obstacles between the sidewalk where they were parked and the street they’d soon be sailing down. How would they do it? How would the truck and its contents make it to the road without hitting the trees, construction equipment, city bicycle racks, or outdoor sculpture? I soothed my anxieties by thinking about the Kakeya needle problem.
I don’t know whether Sōichi Kakeya, the mathematician for whom the problem is named, was a particularly serene person, but the Kakeya needle problem gives me serenity. The problem asks about the minimum area required to turn a line segment (or needle) around while leaving it in the two-dimensional plane. (The needle is assumed to have width zero.)
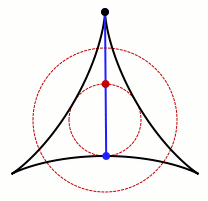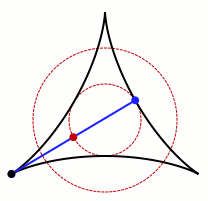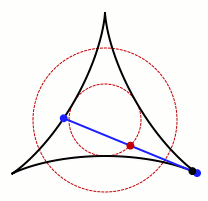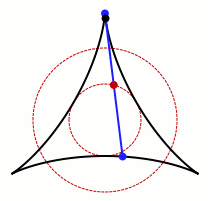
An animation of one set that allows Kakeya's needle to turn around. Credit: Claudio Rocchini Wikimedia (CC BY-SA 3.0)
It’s not hard to see that the process is possible in circles, squares, and equilateral triangles. The gif above also demonstrates that it also works in shapes that are not convex, meaning they bend in.
Kakeya posed the problem in 1917, and Abram Samoilovitch Besicovitch solved it in 1928, showing that there was no minimum area greater than 0. If you turn it slowly enough, over a long enough length, you will be able to get the area smaller than any positive number you want. You can use a pencil to play with the Kakeya problem with your bare hands.
I turn to the Kakeya problem for solace not only when I’m watching a flatbed truck carrying a giant boat do an n-pointed turn but also when I’m behind the wheel of my car and need to turn around in a tight space. I think of the Kakeya problem as the “if you got in, you can get out” theorem for driving, though I recognize that they’re not quite the same. Kakeya’s problem doesn’t care how you got there, and it also assumes your car is infinitesimally thin and you have an infinite amount of length to play with. That is not the case when driving; nevertheless, I allow it to reassure me. At the very least, it’s a reminder to use the space I have and that there’s no shame in adding another point to that turn.
The gulf between theory and practice sometimes feels large, and the Kakeya problem is no different. But as a student who has been asked to “prove or find a counterexample” on a math test could probably tell you, knowing that a problem is soluble can be the difference between making progress and deciding to abandon your car in the back of a narrow parking lot or dead-end of an alley. Because I know that the Kakeya needle problem says there is enough room, I’ll keep inching myself around and eventually make it out. I don’t know whether the flatbed driver moving the boat turned to the Kakeya needle problem for courage, but the boat eventually made it out without incident and sailed into the Paris night.
