This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
A couple of recent adventures in infographics and storytelling have inspired me to contemplate geometric shapes as symbols of humans in society. In the world of science and data visualization, figures such as lines, circles, and rectangles are ubiquitous. Indeed, from points on a scatterplot to bars on a graph, basic shapes often function as the language of visual communication. Sometimes they are even used to represent people. But what happens when the shapes come to life, when they actually become people? As it turns out, humble little polygons may have a lot to teach us about ourselves and the world we inhabit.
Parable of the Polygons
Last week I attended OpenVisConf, an annual Boston-based event centered on visualizing data on the web. Among the stellar list of speakers was Nicky Case, who gave a fascinating talk entitled “How to Simulate the Universe in 134 Easy Steps.” Much of Nicky’s talk focused on visualizing systems as a starting point for understanding our world and promoting social change. “Parable of the Polygons,” an interactive examining racial segregation, is a great example of how visualizing data in a friendly “playable” format can go beyond telling a story and actually motivate users to try to affect change.

Image from "Parable of the Polygons," by Nicky Case and Vi Hart
Click the image to launch the interactive
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
I recommend scrolling all the way through and interacting with the visualization, but for the purposes of this blog post, I’ll sum up the basic premise. The characters in the game, i.e. the triangles and squares, each appear either happy, sad, or “meh.” The user’s role is to move the sad ones around into the available spaces until there are no more frowning faces on the board. The key is that all of the shapes want to be in a relatively diverse environment. The ideal scenario for each individual is that one-third of the shapes in their immediate vicinity look like them. They’ll settle for a higher proportion of neighbors from their own group, but if outnumbered by more than two-thirds, they will frown and wobble until they are relocated. The game ends when all of the shapes are satisfied with their neighbors.

Image from "Parable of the Polygons" after completing the game
One might assume that, since each individual prefers some level of diversity, the groups will end up fairly well integrated. However, since they started out somewhat segregated, and many of them passively accept this scenario (as in many real-world neighborhoods), the result is rather disappointing; it is virtually impossible to avoid pockets of homogeny. Despite each individual being only “slightly shapist,” the system effectively dooms them to a less-than-favorable outcome. A subsequent iteration of the game demonstrates that simply lowering bias against members of the other group doesn’t make a difference. Rather, individuals must reject the default scenario of segregation and actively begin to seek out neighbors who look different from them.
Flatland
The idea of using two-dimensional geometric shapes to represent people in an allegory for society is not new. In 1884, an English schoolmaster named Edwin A. Abbott published the illustrated novella Flatland: A Romance of Many Dimensions. Abbott’s story was originally presented as a social satire about Victorian England, but was later hailed by scientists and mathematicians for its thought-experiment-style investigation of a hypothetical four-dimensional reality.

Cover of Flatland
Written and illustrated by Edwin A. Abbott
Once again, I urge you to read the story yourself—it’s both dryly witty and surprisingly relevant to current social and economic conditions—but in case you can’t drop everything right now just to read a quick novella, allow me to outline some of the key points. The main character is “A Square,” who lives in Flatland, so named because it is a two-dimensional world. Society in Flatland is organized into strict classes based on shape. Males are polygons having a variable number of sides; the more sides an individual has, the higher his class. Thus, the highest social order is made up of circles. Women, however, are all simple lines—the lowest of the low. (Prophetically enough, women are regarded as “deficient in Reason but abundant in Emotion,” denied schooling, and relegated to the home lest an unwitting polygon run into her in the street and accidentally impale himself on one of her pointy ends.)
Ascent through this hierarchy is ostensibly within reach—for males, at least. According to the so-called “Law of Nature,” each successive generation of equal-sided polygons gains one additional side. However, this possibility for advancement eludes most members of the lowest class, the isosceles triangles. Their sides and angles being unequal, they must first ascend to equilateral status—an exhausting challenge met only by the most exceptional among them—before their sons can gain any more sides and improve their standing in the world.
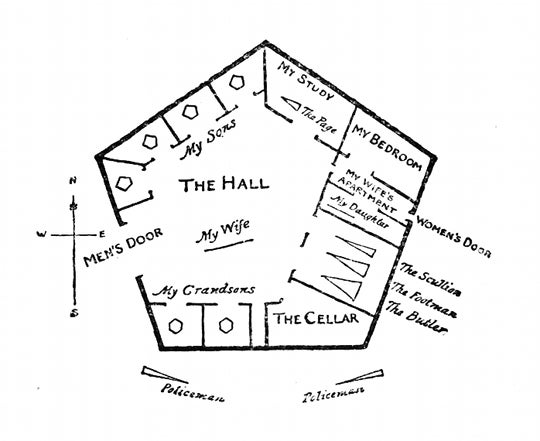
Illustration of A Square’s house in Flatland
The story gets interesting when A Square has a dream that he visits a one-dimensional world called Lineland. He attempts to explain to one of Lineland’s residents (a line) the concept of a second dimension and is met with utter incredulity. (Incidentally, his linear acquaintance turns out to be a king, and is suitably offended that the square initially mistakes him for a woman, who in his world would be nothing but a mere point.) The square returns from his vision vexed by the line’s inability to grasp such a seemingly simple concept.

Illustration of A Square’s encounter with the King of Lineland
Later, on the eve of the new millennium, A Square is visited by A Sphere from Spaceland, a land of three dimensions. Of course, the square is initially flummoxed, unable to conceive of a third dimension. Frustrated by the square’s ignorance, the sphere whisks him off to Spaceland, where he is able to see and experience what the sphere has been attempting to describe in words. Finally, everything becomes clear. Inspired by his new understanding of three-dimensional space, the square begins to imagine worlds where there are four dimensions, or five, or even more. But when he returns to Flatland and tries to communicate these ideas to his fellow polygons, he is met with confusion and disbelief. What’s more, the President of the Council of Circles regards his radical ideas as a threat to the social order, and throws him in prison.

Illustration of A Sphere in Flatland
Interestingly, although Abbott’s astute critique of English society went largely unappreciated during his time, the more science-related themes of the book re-emerged after 1915, when Albert Einstein published his theory of general relativity. Over the years since then, Flatland has been referenced by admiring physicists and mathematicians in various forums, including Scientific American. For example, in 1962, Martin Gardner dedicated his “Mathematical Games” column to analyzing “fiction about life in two dimensions.” And as recently as 2012, Stephen Carlip cited Flatland as he described how gravity would behave in a two-dimensional world.

Graphic from “Quantum Gravity in Flatland,” in March 2012 issue of Scientific American
Illustrations by Malcom Godwin
Common Themes
While “Parable of the Polygons” and Flatland are associated with very different times, places, and even media types, the parallels between them are not hard to find. For example, in both social systems described, the apparent potential for positive change rests on faulty logic. The shapes in “Parable” assume that their individual preference for diversity is sufficient to propel their society toward integration, but it turns out that the social system in which they operate prohibits it. Likewise, in Flatland, the “Law of Nature” purports to allow for social mobility, but due to restrictions on the lower classes, a significant portion of the population remains permanently marginalized, and social justice cannot prevail.
Moreover, in both worlds, true progress requires a more active, dramatic shift than expected. In Flatland, A Square must change his entire conception of space in order to see beyond his narrow, two-dimensional existence; indeed, he must physically leave Flatland and experience another world. Similarly, in “Parable,” the complacent squares and triangles must abandon their preconceptions about the nature of “shapism” and adopt a new, activist stance on integration.
Moral of the Story: Visualization is Key!
To my delight, both of these stories advocate for visualization as the key to understanding the nature of society. “Parable of the Polygons” presents this concept in a more straightforward manner, as the physical arrangement of shapes visibly changes based on the user’s actions. In Flatland, the case for visualization is a bit more conceptual; the square cannot picture a three-dimensional world until he has seen and experienced it. But beyond that, in relating his story, the polygonal narrator provides diagrams for the reader.
Even more tellingly, towards the end of the text, A Square laments his inability to explain three-dimensionality to his peers for his lack of a functional drawing surface. Abbott writes: “So I devoted several months in privacy to the composition of a treatise on the mysteries of Three Dimensions . . . I spoke not of a physical Dimension, but of a Thoughtland whence, in theory, a Figure could look down upon Flatland and see simultaneously the insides of all things, and where it was possible that there might be supposed to exist a Figure environed, as it were, with six Squares, and containing eight terminal Points. But in writing this book I found myself sadly hampered by the impossibility of drawing such diagrams as were necessary for my purpose; for of course, in our country of Flatland, there are no tablets but Lines, and no diagrams but Lines, all in one straight Line and only distinguishable by difference of size and brightness; so that, when I had finished my treatise . . . I could not feel certain that many would understand my meaning.”
So, there you have it. The key to understanding and ultimately changing the world lies in our ability to visualize the systems that govern us. Luckily, our four-dimensional world affords us this ability, and when we seek symbols to represent components of the system, trusty little shapes will be there to help us out.