This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
On a recent episode of our podcast My Favorite Theorem, my cohost Kevin Knudson and I talked with Carina Curto, a mathematician at Penn State University who specializes on mathematics applied to biology and neuroscience. You can listen to the episode here or at kpknudson.com, where there is also a transcript.
Curto told us about the Perron-Frobenius theorem, which comes from the field of linear algebra. As Curto gushes in the episode, linear algebra is one of the workhorses of mathematics. It provides a robust set of techniques for modeling and understanding systems of equations that arise in many different contexts.
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
One of the central objects of study in linear algebra is a matrix. A matrix is an array of numbers, but it’s much more than that. The numbers are arranged in rows and columns and are usually thought of as a shorthand representation for a transformation of a space. For example, one way to transform the plane is to take each point in the plane, written as (x,y) and send the first coordinate, x, to the sum 2x+y and the second coordinate, y, to x+y. The matrix
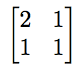
encodes that transformation.
In general, a ray of points emanating from the origin can be stretched and rotated by a transformation encoded by a matrix, but in a special direction called the eigenvector, the transformation is limited to stretching or shrinking. There is no rotation. The amount by which a unit length segment pointing in this direction is stretched or shrunk is the eigenvalue. The Perron-Frobenius theorem states that for a square matrix with all positive entries, there is a unique largest real eigenvalue and that its corresponding eigenvector has positive x and y coordinates.
I vaguely remembered hearing about the Perron-Frobenius theorem before talking with Curto, but I did not initially find it particularly compelling. I learned early in my first linear algebra class not to put too much stock into the numbers you see in a matrix. That is, you shouldn’t think you can understand what a matrix will do based only on what its entries look like. I think part of my failure to appreciate the Perron-Frobenius theorem earlier is that I was a little bit suspicious of a theorem that did allow me to know something about a transformation based on the numbers in a matrix. And to top it off, not many matrices have all positive entries, so what’s the point of a theorem that applies to such an exclusive set of matrices?
Curto convinced me that the theorem is more useful than I gave it credit for. True, there’s no reason to think any arbitrary matrix is going to have all-positive entries, but many applications do deal primarily with all-positive matrices. The matrices that represent functions related to population dynamics, demographics, economics, and web search algorithms often have all-positive entries, so the Perron-Frobenius theorem applies to them. For the current moment, there is even an epidemic model, the Kermack-McKendrick model, that uses the Perron-Frobenius theorem. (My mention of this model should not be construed as an encouragement to take up armchair epidemiology.) Readers and listeners who want a more extensive introduction to the many proofs and applications of the Perron-Frobenius theorem should check out a paper called, appropriately enough, The Many Proofs and Applications of the Perron-Frobenius Theorem.
