This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
Last month, I learned that Indian mathematician Sharadchandra Shankar Shrikhande passed away at age 102. The name rang a bell because not long ago I had learned about “Greco-Latin squares,” the mathematical construction for which he was most famous.
To understand Shrikhande’s work, we have to go back a few centuries to legendary Swiss mathematician Leonhard Euler (1707–1783), who wrote about the problem shortly before his death. (An English translation of his paper about it is here.) A Latin square is an arrangement of n symbol in an n×n array so that each symbol appears once in each row and column. (Sudokus are 9×9 Latin squares that also satisfy additional requirements.) As a side note, in spite of the European name, Latin squares had been investigated before Euler found them, including by Korean mathematician Choi Seok-jeong, who was born about 70 years before Euler.

A Latin square of order 4. Each symbol appears exactly once in each row and column. Credit: Alejandro Vera Temiño Wikimedia (CC BY-SA 3.0)
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
As a point of clarification, although Euler's paper is called "Investigations on a new type of magic square," most math enthusiasts would not call them magic squares today. A magic square of order n×n use each number between 1 and n2 exactly once, while Latin squares use only the numbers between 1 and n, but use each one n times.
A Greco-Latin square is an arrangement of two sets of n symbols in an n×n array so that each set of symbols forms a Latin square and no pair of symbols appears twice. The name can make it a little easier to imagine: the first set of symbols can be the first n letters of the Latin alphabet, and the second set can be the first n letters of the Greek alphabet. Every possible pair of one Latin and one Greek letter must appear exactly once in a Greco-Latin square. The number n is the order of the Greco-Latin square.
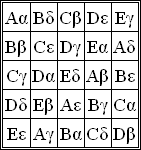
A 5×5 Greco-Latin square using the first five letters of the Greek and Latin alphabets. The Latin letters form a Latin square, as do the Greek letters, and every combination of one Latin and one Greek letter appears exactly once. Credit: Maksim Wikimedia
Euler’s investigations led him to the conclusion that Greco-Latin squares exist for odd orders and orders that are multiples of 4. No Greco-Latin square of order 2 exists (you can check it for yourself), and Euler tried to make one of order 6 without success, leading him to the conjecture that no Greco-Latin squares of order 4n+2 exist. Rigorous proof that no such square of order 6 took a little longer. (Danish mathematician Thomas Clausen claimed he had proved it in an 1842 letter, but that proof has been lost. A 1901 proof by Gaston Tarry is the earliest that still survives.)
Researchers developed ways to construct Greco-Latin squares of certain orders based on squares of smaller orders. For example, a Greco-Latin square of order 4 and one of order 3 could be combined to form one of order 12. But their techniques did not work for orders that had exactly one factor of 2, like 2, 6, and 10, so they did not resolve the question for larger numbers of the form 4n+2.
Finally, in 1959, Shrikhande, Raj Chandra Bose, and Ernest Tilden Parker cracked the code, publishing several papers that resolved the conjecture fully, not only showing that Greco-Latin squares of orders 10, 14, 18, and so on exist, but also producing constructions of them in some dimensions. They earned the moniker “Euler’s spoilers.” (For it to work, you need to know that Euler is pronounced like “oiler,” not “yooler.”) The picture at the top of this post is a colorful example of a Greco-Latin square of order 10.
Greco-Latin squares are mostly just fun, but they have some surprising practical applications as well in designing science experiments. A paper about Greco-Latin squares by Dominic Klyve and Lee Stemkoski notes that Greco-Latin squares (and higher-order similar squares, with not just two but three or more symbols per box in the array) could be used to set up experiments where a number of different test subjects need to compare their performances on several different tests. Check out Klyve and Stemkoski’s article for more about the history of the problem from Euler through work in the decades following the conjecture’s “spoilage.” For more about Shrikhande himself, read this article by Nithyanand Rao, written on the occasion of Shrikhande's 100th birthday.
