This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
Along with π and e, the golden ratio is a numerical celebrity. It is the ratio of side lengths on a very special rectangle. If you take this rectangle and cut the largest square possible off of it, you are left with another rectangle with exactly the same side length ratios as the first one. This construction defines a unique relationship between the lengths of the sides, and any rectangle whose sides have that relationship is called a golden rectangle. If the shorter side of a golden rectangle has length 1, the longer side has length (1+√5)/2, or about 1.618.
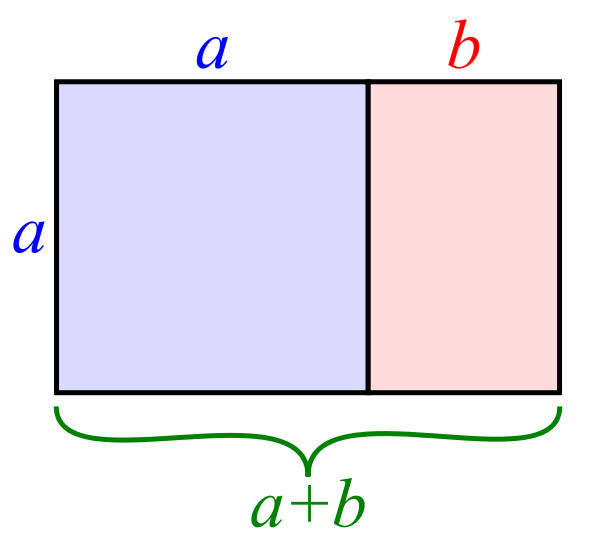
A "golden rectangle" can be cut into a square and another golden rectangle. The ratio of a+b to a is the same as the ratio of a to b.
The golden ratio is familiar to a lot of math enthusaiasts, but have you heard of the silver ratio? What about bronze? These are other similarly constructed irrational numbers that are a little less well-known than their flashy golden cousin. Like the golden ratio, each so-called metallic mean can be visualized as the ratio of side lengths on a special rectangle.
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
For the silver ratio, we want to cut off two squares and be left with one rectangle that has the same aspect ratio as the first one.
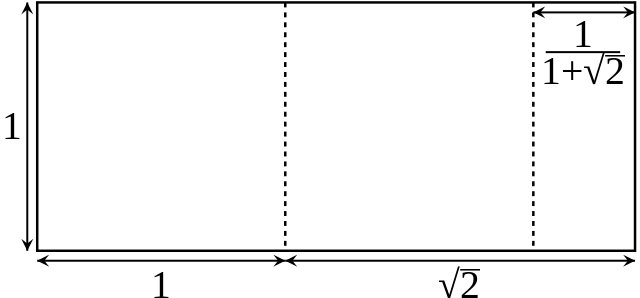
A "silver rectangle" can be cut into two squares and another silver rectangle. The ratio of the side lengths is 1+√2, about 2.414. Image: Krishnavedala, via Wikimedia Commons.
For bronze, we want to cut off three squares and end up with a similar rectangle at the end.
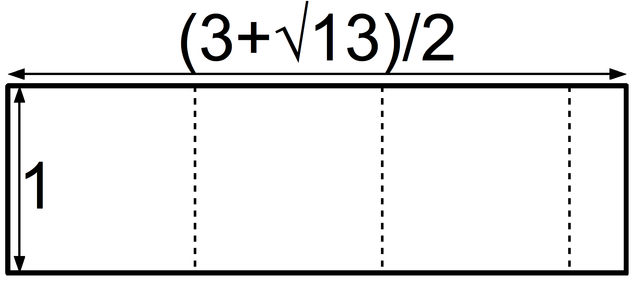
A "bronze rectangle" can be cut into three squares and another bronze rectangle. The bronze ratio is (3+√13)/2, around 3.303. Image: Hyacinth, via Wikimedia Commons.
Other than gold, silver, and bronze, there isn’t a canonical ordering of metals by preciousness or desirability, but we can keep creating these ratios. We might call the next one the copper ratio. A "copper rectangle" could be cut into four squares and another copper rectangle, and the copper ratio would be 2+√5, or about 4.24.
As we keep going, perhaps to nickel or aluminum next, the rectangles will get longer and longer, so it's not too hard to see that each metallic mean is larger than the last one, and just like the golden ratio is between 1 and 2, the silver ratio is between 2 and 3, the bronze ratio is between 3 and 4, and the pattern continues: the nth metallic mean is always between the whole numbers n and n+1.
The golden ratio has an interesting relationship with the famous Fibonacci sequence 1, 1, 2, 3, 5…, in which each term is the sum of the two previous terms. As the terms of the Fibonacci sequence increase, the ratio between successive terms approaches the golden ratio. Likewise, the other metallic means have these relationships with other sequences. For the silver ratio, it’s the Pell sequence. It starts 0, 1, 2, 5, 12, 29…. The nth term is the sum of the (n-2)th term and 2 times the (n-1)th term. For the bronze mean, the formula has a 3 instead of a 2, and so on.
I learned about the metallic means when I was talking to University of Wisconsin-Madison applied mathematician Jean-Luc Thiffeault about taffy-pullers. In a recent paper, he did a mathematical analysis of historical taffy-puller patents, categorizing them based on how much they stretch the candy during each trip through the puller. So if you doubled the length of the taffy each time you stretched it, you’d have a stretch ratio of two. He found that some taffy pullers have stretch ratios based on the golden and silver ratios.
You can actually see the relationship between the golden ratio and the Fibonacci sequence at work in a golden ratio taffy-puller patent from 1918. The motion of the gears means that each turn of the handle will basically add the two previous steps together. If our original taffy blob (top left corner of the below picture) has length 1, the next step will have length 2. Then the next step has length 3, the next is 5, and so on. Over time, the stretch ratio will tend toward the golden ratio, and we can see how the Fibonacci sequence steps get us there.
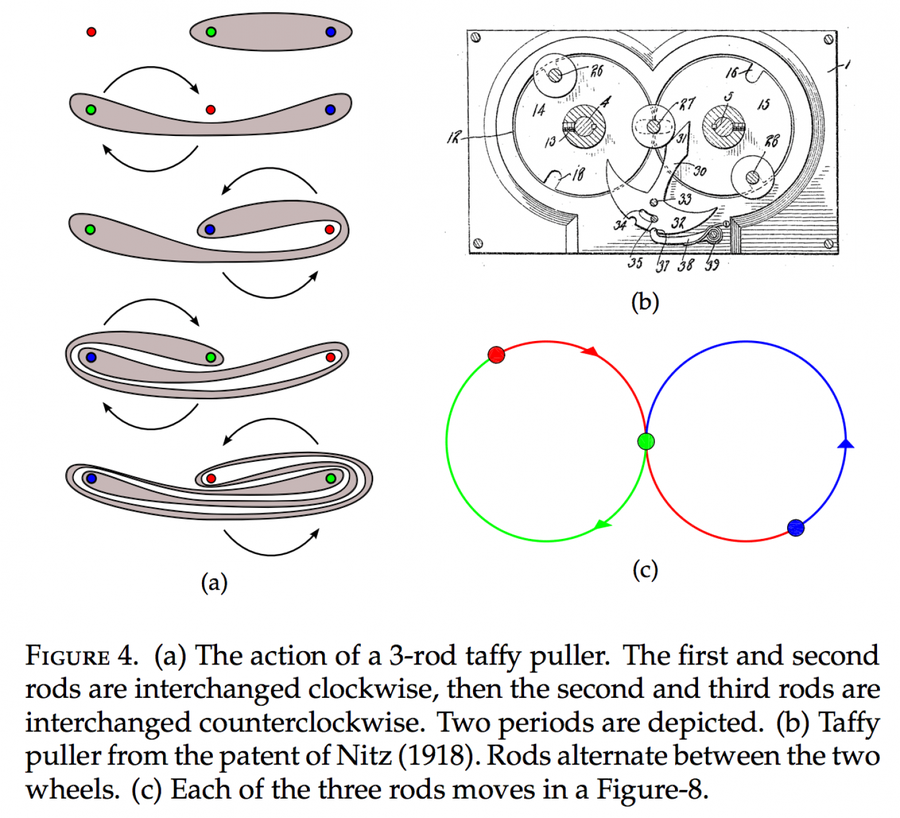
Read more about the mathematics of taffy-pulling in my article on the Smithsonian website.
