This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
In 2003, as a sophomore in college, I was happily sinking more and more deeply into both music theory and mathematics. As befits my personal brand, I wrote a 12-tone serial setting of one statement of the fundamental theorem of calculus for an assignment in a 20th century music class.
Twelve-tone serialism, as Vi Hart explains in an excellent video below, was proposed in the early 20th century to encourage composers to break free of traditional tonality and write music in which no note is more important than any other notes.
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
A serial composer starts with a tone row, which is an ordering of the twelve half steps (or 12 piano keys: C-C#-D-D#-E-F-F#-G-G#-A-A#) in an octave.
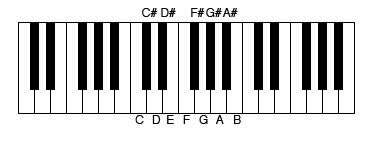
A sketch of a keyboard showing the 12 pitches that make up the notes in a 12-tone row. Credit: Evelyn Lamb, based on Spindoktoren Wikimedia (CC BY-SA 3.0)
The tone row I used in my composition was F#-A-E-D-C#-F-B-G-G#-A#-D#-C.

My tone row, notated on a staff. Credit: Evelyn Lamb
That row and certain modifications of it, such as transposing the row so it starts on a different note or playing it backwards, provide the allowable material in the piece. The composer must use the pitches from one of these rows, in any octave, in order before reusing the earlier pitches. (Some composers interpret the rules slightly differently, but that's the gist.) This is the first line in the vocal part of my song.
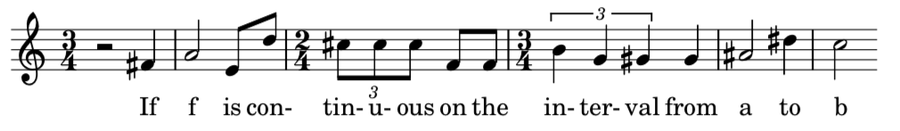
Credit: Evelyn Lamb
My composition was by no means a work of genius (to listen to a 12-tone serial work of genius, check out Alban Berg's Lyric Suite), but my tone row is pretty nifty, if I do say so myself. The beginning and ending sets of four notes evoke traditional tonality, but the row as a whole is craggy enough to keep things interesting. But I was particularly proud of another feature of the row: like one of the main rows in the Lyric Suite, it contains all the possible intervals between two notes in a 12-note system. (Logically enough, such a row is called an all-interval row.)
If you’re not already familiar with the names of musical intervals, it’s no big deal. If you can imagine playing the notes on a piano, you can count the piano keys to tell you the intervals in terms of half steps. The first interval in my tone row, F#-A, is an ascending minor third or a descending major sixth, depending on whether the composer chooses the A to be higher or lower than the F#. For practicality, I’m going to always refer to the number of half steps in the ascending version of the interval, so F#-A is an interval of 3 half steps. The next interval in the row, A-E, is an ascending perfect fifth, 7 half steps. The interval E-D is 10 half steps, and so on. The full sequence of intervals in my tone row is 3-7-10-11-8-6-1-2-5-9. Each interval between two successive pitches is different, meaning each possible interval from 1 to 11 occurs somewhere in there.
I was proud of finding this all-interval row, and the discovery made me want to find more all-interval rows and figure out how to characterize them. Eventually I started noticing some constants in the rows I found: the tritone (the interval of 6 half steps, in the case of my row, between the F and B) was always exactly in the middle, and the intervals had a nice symmetry. The first interval was 12 minus the last interval, the second interval was 12 minus the second to last interval, and so on. Another way to think about this property is that the row played in reverse has the same intervals as the original version of the row.
Having noticed these patterns, I began trying to prove mathematically that every all-interval row must have the same properties. I kept getting stuck. Granted, I was not particularly mathematically sophisticated at the time. I had just started taking an introduction to proofs class, and my mathematical skills were much more computational than theoretical. But what I lacked in sophistication, I made up for with time. I spent a lot of time on the problem and got nowhere. Eventually I moved on with my life, but the problem kept nagging me. For years, I would come back to it every once in a while when I had some paper and a strong desire not to work on whatever I was supposed to be doing at the time. Still nothing.
Finally, a couple years ago, I decided to give up and see if anyone else had proved this theorem for me. I found, to my shock, that the matter had been investigated in 1965, and I was wrong! (I had forgotten that crucial part of trying to prove a theorem: you should spend part of your time trying to disprove it!) In a Perspectives of New Music paper called “On Eleven-Interval Twelve-Tone Rows,” Stefan Bauer-Mengelberg and Melvin Ferentz detail their computer-assisted path to enumerating the all-interval rows.
The paper has some lovely little details in it. In a footnote, the authors describe some familiar feelings:
The problem of obtaining the interval rows by a procedure other than one involving elimination has proved to be highly contagious, and throughout 1963, the authors and many of their colleagues kept reinfecting one another. In their fever states, they produced numerous hypotheses, most of which turned out to be false…
I felt vindicated to learn that two of those hypotheses were the same as mine: an all-interval row would have the same intervals when read forward or backwards, and the tritone would have be in the middle. (They write of the former conjecture, “strong evidence in its favor was the fact that [composer and music theorist] Milton Babbitt could not instantaneously come up with a counterexample.”) But IBM researchers looking into the question gave them two counterexamples:
C-B-D#-F-G#-C#-G-E-D-A-A#-F#

A counterexample tone row. Credit: Evelyn Lamb
C-D#-E-A-B-A#-G#-F-C#-G-D-F#

A second counterexample, shattering all my big dreams. Credit: Evelyn Lamb
In the first counterexample, the tritone (between C# and G) is in the middle of the row; in the second, the tritone (also between C# and G) is the third interval from the end.
Bauer-Mengelberg and Ferentz translated the musical conditions into a math problem about permutations and wrote a computer program to find all the permutations that could generate all-interval rows. After seven minutes and twelve seconds crunching on an IBM 7094, there were 1,928 such permutations, each of which could be used to create 24 different all-interval rows for a grand total of 46,272 all-interval rows out of a total of 479,001,600 possible tone rows, or about 1 in 10,000 (coincidentally, similar to the odds that a family with 14 children will have all boys).
Bauer-Mengelberg and Ferentz expected to find simple mathematical conditions that would allow one to find and characterize all the all-interval rows. Instead, after some basic simplifications, their method to find the rows boiled down to brute force, listing possible permutations and tossing out the ones that didn’t have the required properties. This lack of results struck them as noteworthy. They write, “In fact, perhaps the most interesting result thus far obtained is that these structures, whose mathematical characterization, as we shall see, is quite simple, should in some ways be so very recalcitrant to analysis.” I'm so glad it wasn't just me!
Later investigations, including “The Structure of All-Interval Series” by Robert Morris and Daniel Starr, have provided some alternative ways of classifying and generating all-interval rows, but they are still somewhat enigmatic. There is no easily human-implementable recipe to generate them, and they don’t all have the same properties. I’m relieved that I finally found closure in my quest to mathematically characterize the all-interval rows, even if it’s because I was wrong.
