This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
In a new Android ad, a pianist plays two pianos. One is a normal piano, and one has all the strings tuned to the same note, a middle C.
Naturally, after watching the commercial, I wondered how they made the piano do that. According to the “Making of Monotune” video embedded above, they modified the innards of the piano to change a lot of the string lengths. I respect that it was a difficult technical undertaking, but frankly, that’s kind of a boring answer. What if they had tried to tune every note on the piano to middle C without modifying the strings or inner workings of the instrument?
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
If you’ve ever peeked inside a grand piano, you’ve seen a mess of strings that vary in length and thickness, getting shorter and thinner as you go from lower to higher (left to right). The pitch of a vibrating string depends on its length, its density (which generally corresponds to its thickness), and the tension placed on the string. Lengthening or thickening the strings lowers the pitch, while increasing the tension raises the pitch. The precise formula for the frequency (f) of a note on a vibrating string based on length (L), tension (T), and density (μ) of the string is shown below.
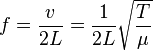
In theory, you can tune a string of any length and thickness to any pitch by adjusting its tension, so in theory, you can tune any string on a piano to any pitch. How much tension would you have to apply to do that?
Pianos from uprights to concert grands all produce the same pitches on instruments of vastly different sizes, so there is no one standard for the lengths and densities of piano strings. But we don’t need to know those quantities at all. We can just look at the relationship between frequency and tension and see that if we hold length and density constant, the frequency is proportional to the square root of the tension.
A middle C has pretty close to 10 times the frequency of the lowest note on a piano, so we would need about 100 times the tension to tune the lowest string all the way up. It’s safe to say that tuning the string that way would not be good for your piano. In all likelihood, the string would break long before you tightened it all the way. If somehow the string managed to hold out, it would go from needing around 200 pounds of tension to 20,000 pounds, the difference between being able to hold a smallish football player and an entire football team. The total tension on a piano tops out at around 45,000 pounds spread over the 88 keys of a Steinway concert grand. Concentrating half that tension on just one string would probably rip the instrument apart. Never mind the fact that many of the other low strings would need almost as much tension, so the left side of the piano would have several football teams pulling on it.
On the other side of the keyboard, we’d also have problems tuning the highest strings down to a middle C. We wouldn’t risk destroying the piano, but there’s a good chance the strings would not make a sound. The high C on a piano is 4 octaves above a middle C, so its frequency is 16 times the frequency of the middle C. That means we’d need to reduce the tension to 1/256 of the tension it normally has. Based on my experience playing a stringed instrument, I don’t think the string would make any noise at all with that little tension. It would be like trying to strum the fringe on a scarf.
After running the numbers, I am quite convinced that changing the guts of the piano is the right call if you want to tune all the keys to the same note. And why would we want to do that anyway? The Android ad vividly demonstrates that sacrificing all variation in pitch makes music, or at least the third movement of Beethoven's Moonlight Sonata, much less rich, but it ignores one big advantage: this is one piano that could actually be in tune.
