This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
Look at giraffe’s fur and you’ll see a collection of irregular brown spots that fit together like puzzle pieces. The delicate veins on a dragonfly’s wings also outline a puzzle-like collection of irregular translucent cells. And the honeycomb cells built by bees also appear to fit together, although in this case arrangement is regular. All these natural patterns may be modeled with a mathematical technique known as a Voronoi tessellation.
.jpg?w=560)
Figure 1. Dragonfly wing. Credit: Joi Ito Flickr(CC BY 2.0)
“Many times, the patterns you see in nature are Voronoi tessellations,” says Javier Buceta, a member of a team of Spanish, British, and American researchers that recently sought to predict the shape of epithelial cells—the cells that line the surfaces of our skin, intestines, blood vessels, and organs. Given Voronoi tessellations’ prevalence in nature, Buceta and his colleagues used this mathematical model to predict the shape of epithelial cells, which among other things make up the surface of your skin and the inside of your throat, intestines and blood vessels.
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.

Figure 2. Honeycomb. Credit: Giuliagi Wikimedia(CC BY-SA 3.0)
The model indicated that epithelial cells should take the form of an unusual and previously unknown shape they named the “scutoid.” Of course, epithelial cells in nature were under no obligation to observe the model, especially as the oddly-shaped, not-previously-observed scutoid seemed like an unlikely candidate. Imagine the researchers’ surprise, however, when their microscopes revealed that scutoid-shaped epithelial cells were pervasive in the human body, news they published last July in Nature Communications.
“Even kindergarteners know how to make Voronoi tessellations. Throw some candy in a kindergarten classroom where children are randomly playing. Once the candy lands, tell the kids to run to the candy that is closest to them,” said Buceta. His kindergarten Voronoi tessellation example might be illustrated with the diagram in Figure 3. The black dots, which depict the scattered candies, are the “sites” of the tessellation. The nonoverlapping shapes with straight sides—polygons—depict the regions in which kids may stand at the start are the tessellation’s “cells.” Any kid inside an individual cell is closer to the candy (the site) in his or her cell than candies (sites) in any other cells.
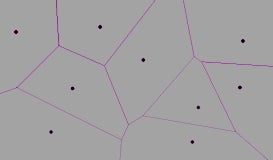
Figure 3. Voronoi diagram. Credit: Jaymz Height-Field Wikimedia (CC BY-SA 3.0)
Also, a kid on a boundary line is equidistant to candies in neighboring cells. In this game, when a kindergartener scans the room and identifies the piece of candy—his site—to which he is closest, Buceta says the child is modeling the situation with a Voronoi tessellation. When the kindergartener identifies some classmates he expects to run to “his” piece of candy and others he expects will run to other pieces of candy, he is drawing a mental Voronoi tessellation map.
The pattern in Figure 3 resembles the irregular patterns on giraffe fur and dragonfly wings as both may be modeled with Voronoi tessellations. Bee honeycombs may be modeled with Voronoi tessellation sites that are placed in a regular pattern.
Three-dimensional Voronoi tessellations are constructed analogously, except the sites are scattered in 3-dimensional space and the cells around them are 3-dimensional shapes with flat sides. Imagine a box filled with bubbles—the cells—that expand to meet in planes. Any point inside a bubble is closer to the site of its bubble than the site of any other bubble. The tightly-packed, scutoid-shaped epithelial cells that line skin, intestines, blood vessels, and organs are the cells in a three-dimensional Voronoi tessellation.

Figure 4. Scutum of a beetle. Credit: Laisverobotams Wikipedia
The researchers derived the word “scutoid” from the scutellum of beetle—see Figure 4–as the two share attributes. A scutoid is more complicated than a prismatoid, which is more complicated than a frusta, which is more complicated than a prism.
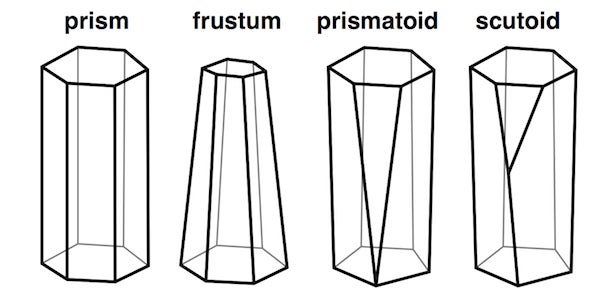
Figure 5: 3-D Voronoi tesselations. Credit: Wikimedia(CC BY-SA 4.0)
Everyone uses Voronoi tessellations, even without realizing it. Individuals seeking the nearest café, urban planners determining service area for hospitals, and regional planners outlining school districts all consider Voronoi tessellations. Each café, school, or hospital is a site from which a Voronoi tessellation is generated. The cells represent ideal service areas for individual businesses, schools, or hospitals to minimize clientele transit time. Coffee drinkers, patients, or students inside a service area (that is, a cell) should live closer to their own café, hospital, or school (that is, their own cell’s site) than any other. Voronoi tessellations are ubiquitous, yet often invisible.
When news of the scutoid broke last July, the New Yorker published an essay, “We Are All Scutoids: A Brand-New Shape Explained,” that described the scutoid as a “column with half of one end lopped off at an angle…a twisted prism…a prism with a zipper.” The comedian Stephen Colbert, in his opening monologue on The Late Show, referred to the scutoid as a “hot, new shape that is burning up the internet” and joked that it was made by “the crack team at Fisher Price University.” The scutoid was featured in a National Public Radio Wait, Wait, Don’t Tell Me limerick:
Picture hexagons with a long cape.
Tack a triangle on with some tape.
Science informs us this find is enormous.
They claim they have found a new...shape.
Popular press coverage seemed to suggest that scutoids were a passing fad. However, don’t be fooled; scutoids and the Voronoi Tessellations that gave rise to them have been with us all along and will continue to be, if only we are willing to see.