This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
Salvador Dalí once went shopping for a scuba suit, and the clerk asked how deep he planned to dive. He answered matter-of-factly, presumably stroking his “10 past 10” mustache: “to the depths of human consciousness.”
Salvador Dalí was no stranger to abstract thinking, but it extended beyond his public persona and his absurd mustache. He spent a lifetime collaborating with mathematicians and scientists; this confluence of fields inspired some of the artist’s most enduring works.
His 1954 painting Crucifixion (Corpus Hypercubus) bears the most obvious evidence of mathematical influence. The painting depicts Jesus levitating in front of a cross, albeit one that appears to be made of cubes rather than flat boards and seems to span three dimensions rather than two.
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
The catch here is that the hypercubus in the painting’s title refers to a four-dimensional object.
A dimension in this sense is usually defined as a degree of freedom of motion (note here that I am talking about spatial, not temporal, dimensions). One way we are free to move is left-right, another is forward-backward, another is up-down. Three spatial degrees of freedom, thus, three spatial dimensions. This sets the background environment.
Now, let’s think about objects of different dimensions which exist in our three-dimensional space. Start with a one-dimensional object, like a line. To build up to the next dimension, the usual move is to add a line perpendicular to the previous line. If you connect these in a particular way, you have a square (a two-dimensional shape). Then, draw lines perpendicular to the square, connect them in a particular way, and you end up with a cube (a three-dimensional shape). Finally, draw lines perpendicular to all faces of the cube, and you’ve got yourself a four-dimensional version of a cube, called a “hypercube.” Visualize it. Really picture it. Simple, right? If you answered “yes,” there’s a large chance you’re lying to yourself.
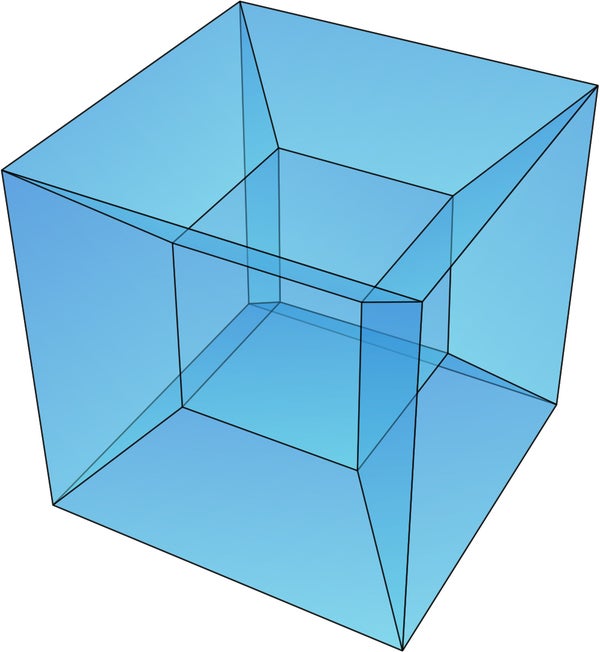
Projection of a hypercube, the four-dimensional equivalent of a cube. Dali used an "unfolded" representation of a hypercube in his painting Crucifixion. Credit: Mouagip Wikimedia(CC BY-SA 3.0)
David Foster Wallace wrote about trying to visualize the fourth spatial dimension: “you can feel, almost imperceptibly, a strain at the very root of yourself, the first popped threads of a mind starting to give at the seams.” Perhaps this explains Salvador Dalí’s mustache? Most of us can’t expect to truly make sense of dimensions outside of our three-dimensional realm of experience, but we can do something to bring it closer to home. We can mentally “unfold” the four-dimensional hypercube—the mathematical equivalent of breaking down a box. The act of breaking down a box knocks the box down from being a three-dimensional object to an (approximately) flat two-dimensional object.
When a three-dimensional cube is unfolded to two dimensions, the result is a cross made of squares; when a four-dimensional hypercube is unfolded to three dimensions, the result is the shape in front of which Jesus levitates in Dalí’s painting.
Twenty years after the Metropolitan Museum of Art hung Crucifixion, the Washington Post ran a feature on Thomas Banchoff, a Brown University mathematician who was studying the fourth dimension. The article included a small photo of Crucifixion, which was printed without Dalí’s permission. A few days after the article was published, Banchoff received a phone call demanding that he come to New York for a meeting with Salvador Dalí himself. Banchoff assumed it was either “a hoax or a lawsuit,” but nonetheless agreed.
Banchoff got on a train, and, hours later, two men from seemingly disparate worlds met at a hotel bar in New York City. This was the beginning of a lifelong collaboration. Dalí and Banchoff discussed the nuances of four-dimensional geometry and other cutting-edge mathematics, and they continued to meet regularly until Dalí’s death in 1989.
Banchoff was one of Dalí’s many partners in the scientific and mathematical communities. These influences appear in much of his work, ranging from themes of quantum mysticism and DNA to his use of stereoscopic painting techniques. When Dalí died, he was collaborating with Banchoff on plans for a highly mathematical sculpture that, had it come to fruition, would have placed a horse’s rear end on the moon.
Whether or not Salvador Dalí’s mind ever fully “gave at the seams” is up for debate, but by the end of his career he was one of the most celebrated painters of the 20th century. A lifetime of pursuing what some people consider to be opposing intellectual territories led him to create some of his most renowned works.
Still, it’s good that he purchased a suitable scuba suit, as he remarked later in life “I am a carnivorous fish, swimming in two waters. The cold water of art and the hot water of science.”