This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
Someone asked me recently why it's only black holes and compact objects like neutron stars that produce gravitational waves.
The answer is that it isn't only these objects.
The gravitational wave signals detected by LIGO do come from the inspiral of pairs of black holes. But, in simple terms, all moving, accelerating, asymmetrical objects can generate ripples in space that will carry energy away. The extreme compactness of black holes is what allows them to generate enough wave energy to not only be (just) detectable by our instruments, but to also inspiral on cosmically short timescales as that energy is lost to the cosmos.
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
Binary stars emit gravitational waves, stars and planets do, and even a pair of waltzing humans are radiating into the 'fabric' of space - albeit with a power level that is absolutely miniscule.
Specifically, the power being lost into gravitational waves by a pair of objects of masses m1 and m2, orbiting around their common center of mass in circular paths is given by:
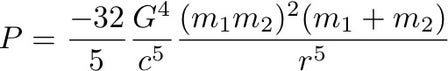
If we plug in values for the Earth-Sun system (with its orbital separation r) the power being radiated away in gravitational waves is about 200 Joules per second (200 watts).
That might actually sound like quite a lot, until you compare it to the total kinetic and potential energy of the Earth in the Sun's gravitational field, which is roughly 1036 joules. So, over the course of a single orbit the total energy loss due to gravitational waves would be roughly equivalent to a shift in Earth's orbital radius of 10-13 centimeters.
Another way to look at this is to ask how long it would take for two orbiting objects to inspiral due to gravitational wave energy loss. The basic formula for this timescale (in handy units of orbital radius 'a' in AU and masses in solar masses) is:
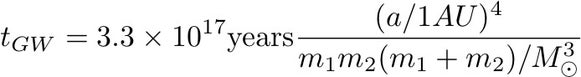
If the Earth and Sun had no external influences, and if the Sun remained the way it is today (rather than inflating in a few billion years and essentially wiping out the inner planets of the solar system), and if we ignore other tidal force effects, the pair would take roughly 1023 years to inspiral due to gravitational wave energy loss.
That's quite a while; a leisurely hundred billion trillion years into the future.
Even an extreme planet-star configuration of a hot Jupiter orbiting a solar mass star at a mere 0.01 AU only gets us into the realm of a few trillion years inspiral due to gravitational wave radiation.
So, the simple answer is that gravitational waves are being produced all around us, all the time. They're just really, really low energy compared to what happens with the universe's most compact and massive objects.
