This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
There are 101 non-fiction, and several fiction, books credited to popular science and mathematics writer Martin Gardner (1914-2010) , who would have turned 101 on October 21. Among the myriad math problems that Martin presented in his influential Mathematical Games column in Scientific American over a 25-year period, quite a few of them spawned more questions than answers, which is actually a good thing.
The influence of the Mathematical Games brand and recognition of the importance of recreational mathematics continues today, and Martin’s readers now span several generations. His hard core fans continue to host invitation-only “Gatherings for Gardner” in Atlanta every two years and anyone (anywhere) can attend or host Celebrations of Mind in and around each October. Most importantly, people keep pushing the envelope by producing new solutions of substance to his conundrums as well as new twists on old plots.
Below, we take a romp through some intuitively appealing two-dimensional dissection and tiling breakthroughs that Martin initially got his readers excited about. It’s pleasing to note that some of the results are quite recent, confirming Martin’s conviction that recreational mathematics can lead to real ongoing research in addition to forming a natural springboard for curiosity and innovation.
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
Triangles and Squares
Dissections concern the breaking up of familiar shapes into a finite number of interesting smaller pieces, and tilings deal with the dual notion of filling up an infinite space with copies of some particular shape or shapes.
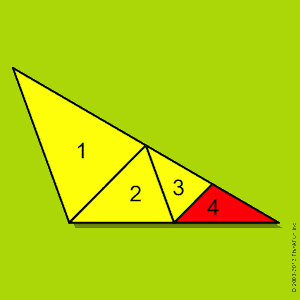
Here’s an easy dissection problem that Martin posed in his February 1960 column: “Given a triangle with one obtuse angle, is it possible to cut the triangle into smaller triangles, all of them acute?” Certainly, initial attempts such as the one shown at right fail (small triangle 4 is not acute).
Here’s a harder one from his April 1981 column: “What is the smallest number of nonoverlapping acute triangles into which a square can be divided?” The surprising solution is original to him. Another puzzle from 1989 that remains unsolved to this day, credited to Richard Guy, who just celebrated his 99th birthday with a chopper flight to the top of Mount Assiniboine, asked if it is possible to triangulate a square with whole number side lengths such that the resulting triangles also have whole number side lengths? As Richard remarked in an email this month, we still don’t know if it’s possible to find a point in the plane of a unit square at a rational distance from each of the four vertices.
In November 1958, Martin asked if a square could be dissected into a finite number of smaller squares of different (whole number) sides, avoiding rectangular subsets—checkerboard patterns and the like are of no interest here. Since the 1930s, it had been known that this was related to electrical network theory. The near solution that Martin offered—a 32x33 rectangle dissected into squares—graced the cover of the magazine that month (the first of a dozen such covers).
It took 20 years for proper “squares of squares” solutions to be found, one of those being a square of side 112 units which is subdivided into 21 squares as required. A compelling elementary argument Martin gave as to why nothing along these lines would work in three dimensions—meaning a cube can’t be broken up into a finite number of unequal cubes—has stuck with me since first reading it 40 years ago. It follows that it won’t work in any higher dimension either!
Let’s now think outside the square, literally, by switching to tiling. In October 1979, Martin wrote about a 1975 challenge put forth by his old friend Sol Golomb: Can the whole infinite plane be tiled by squares, one for each whole number side (1, 2, 3, 4 ... )?
Golumb’s challenge resisted all attacks until Jim Henle and his son Fred conquered it in 2008. Jim explains: “The key to the proof is a lemma stating that given any ell-shaped region it is possible to add squares to form a rectangle. The animation below shows how this is done when starting with the ell formed from a 28x28 square and a 17x17 square.” (The squares are displayed expanded to 3Ds cubes for ease of visualization.)
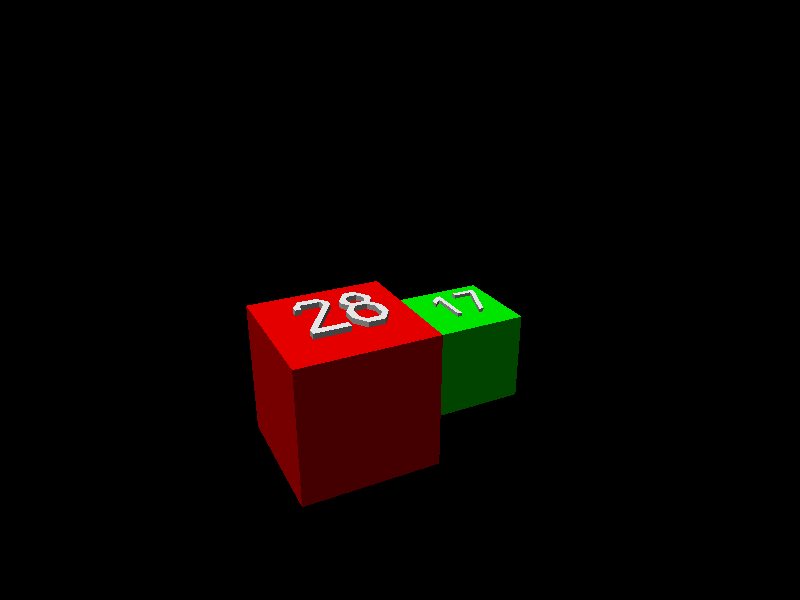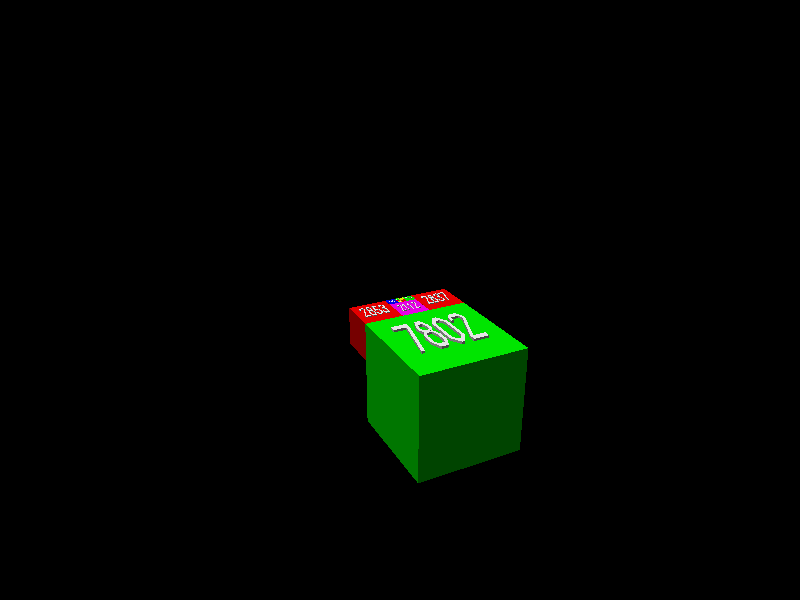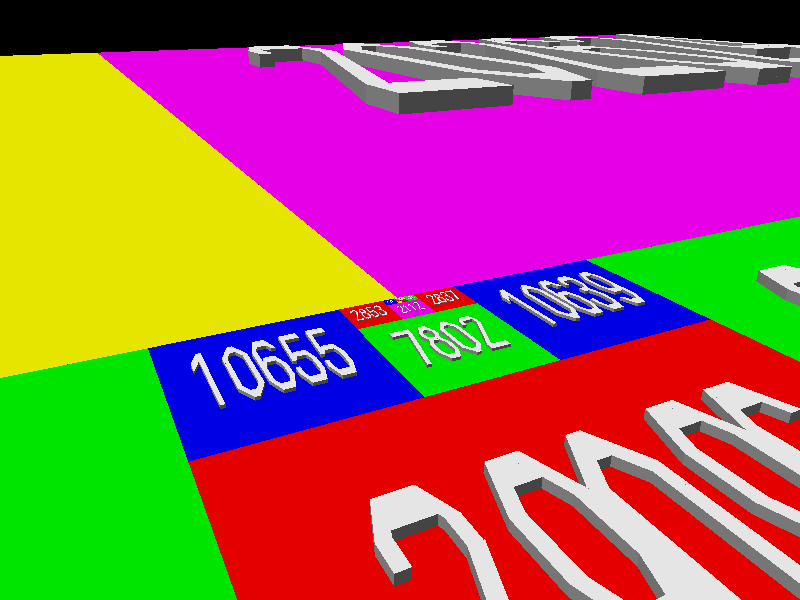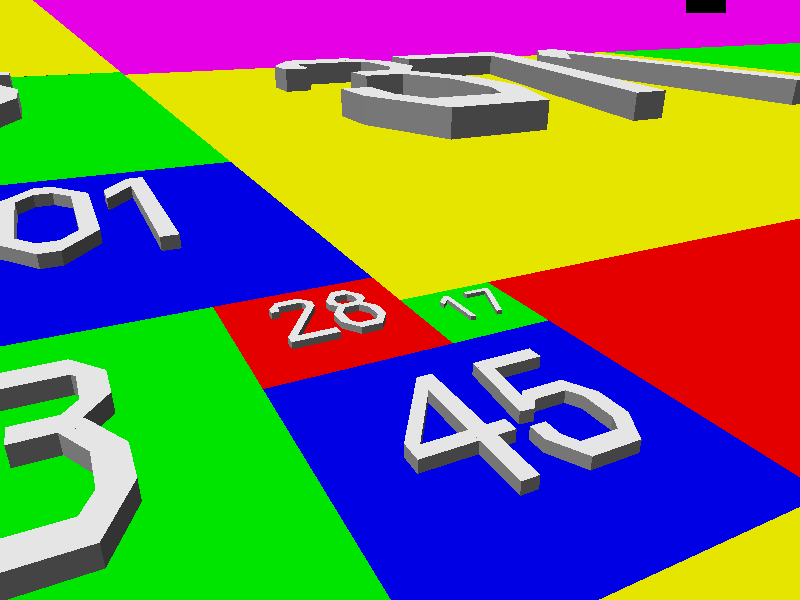
Courtesy of Jim Henle.
Henle continues: “The proof follows easily from the lemma, since once a rectangle is formed, you can take the smallest square not yet in the tiling and add it to the rectangle, forming another ell (which can then be enlarged with more squares to form another rectangle, and so on.” Hence, squares of each possible whole number side will be generated as missing ones are accounted for, and the plane (above the cubes) will be completely tiled.
At the end of their paper the authors discuss the possibilities for tiling the plane with triangles subject to similar constraints, mentioning another still open problem: “Can the plane be tiled with all rational equilateral triangles so that no triangle has an infinite number of neighbors?”
In another devious brainteaser, Martin displayed the following dissection of a triamond into four congruent convex pieces and asked for a dissection of a square using five congruent convex pieces.
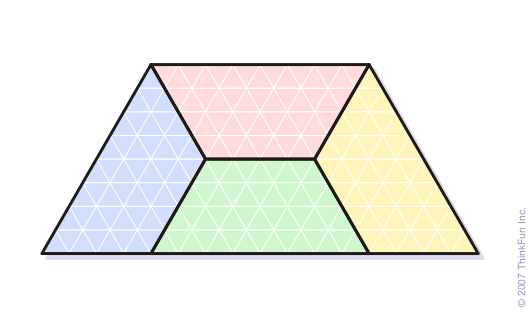
The answer, in hindsight, is blindingly obvious—did we mention that Martin was also an ace magician, and hence a master of misdirection? Yet it was only last month (in the preprint “Dissecting the square into five congruent parts” by Liping Yuan, Carol Zamfirescu &Tudor Zamfirescu) that a proof that no other solution exists was announced.
The ever-surprising Pentagon
Moving beyond three- and four- sided polygons takes us to pentagons, namely five-sided shapes. Regular convex pentagons can’t tile the plane by themselves—as perfectly symmetric triangles, squares and hexagons can—but irregular pengaons can do the job. The possibililties indicated below can all be explored at the interactive Wolfram Pentagonal Tilings Demontration Project site. The story began a century ago, when Karl Rheinhardt found five different types of pentagonal tilings. Here are two of them:

Left: Type 1 pentagonal tiling (Tomruen/Wikimedia). Right: Type 2 pentagonal tilling (Tomruen/Wikimedia)
Fifty years later, in 1968, Richard Kershner found three more types, and following Martin’s coverage of that in his July 1975 column, Richard E. James found another type. Martin duly reported on that in a followup column, and middle- aged San Diego housewife Marjorie Rice read it in her son’s copy of the magazine. Despite having no mathematics training, she set to work exploring and organizing her thoughts and inventing her own notation to keep track of her discoveries. By 1977, she had taken the mathematical world by storm by discovering four completely new types of pentagonal tilings of the plane previously missed by everyone else, two of which are shown below:
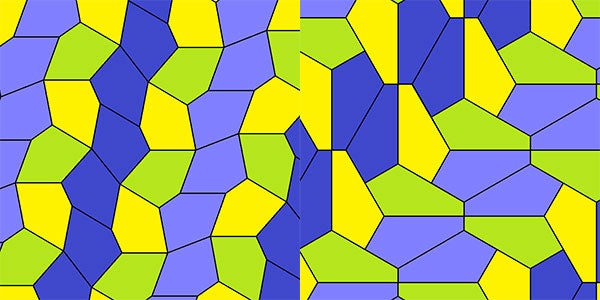
Left: Type 9 pentagonal tiling (Tomruen/Wikimedia). Right: Type 13 pentagonal tilling (Tomruen/Wikimedia)
One of her tilings—discovered in 1995—was used for a floor tiling at the Washington, D.C., headquarters of the Mathematical Association of America, as adapted by mathematician Doris Schattschneider.

In 1985, Rolf Stein found one more type of pentagonal tiling, bringing the total to 14 types. Thirty years went by before Casey Mann, Jennifer McLoud and David Von Derau, all at the University of Washington Bothell announced a 15th type last July. Here is one incarnation of it:

Type 15 pentagonal tiling. (Tomruen/Wikimedia)
Below are all 15 tiling types on one place, for ease of comparison, in a new panel as supplied by the Bothell team:

Are there additional types of pentagonal tiling yet to be discovered? If so, how many might there be? Jennifer McLoud, a Native American and the first in her family to earn even a bachelor's degree, points out that, “There is no known upper bound on the number of ways to tile the plane with convex pentagons.” In other words, there might be dozens more pentagonal tiling types—or even infinitely many. Or maybe no more at all.
Nailing the Coffin
It’s instructive to take a close look at the Bothell pentagon, which resembles an irregular coffin. Perhaps McLoud and colleagues really have nailed it, by discovering the last possible type of pentagonal tiling!
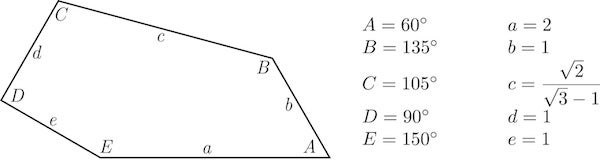
Courtesy of the University of Washington Bothell
Indulge us while we (ahem) pursue the following angle: this shape can be obtained by starting with a hinged horizontal 5-unit long straight stick CDEaAB, [here “a” refers to the midpoint of the segment EA in the image; it also refers to the length of EA], which is then adjusted as follows.
On the right, swing AB counter-clockwise 120 degrees, so that the angle A is 60 degrees. On the left, swing CD clockwise to a vertical position, then keeping angle D at 90 degrees, also swing DE clockwise 30 degrees. EaA remains straight, and is 2 units long. Finally connect ends D and B: It turns out that DB has length sqrt(2)/(sqrt(3)-1), which is roughly 1.93 units, and angles C and B are respectively exactly 105 and 135 degrees. The pentagram can be decomposed into an isosoles triangle, and equilateral triangle and a quadrilateral with “nice” angles.
A kid fooling around with a straw bent in a few key places, suitably spaced out, could easily come up with this pentagonal shape. Perhaps, over the course of time, several have. If so, none realized the significance of their discovery, dropping it without another thought as soon as dinner was announced. And who is to say that some child hasn’t bent straws into other new pentagons that can also tile the infinite plane? It’s the kind of child’s play a grown up could also engage in.
Martin’s most recent posthumous book is certainly child-friendly, with adult undertones. The Annotated Alice: 150th Anniversary Deluxe Edition (W.W Norton), is a final updating of the bestselling volume is his catalog, incorporating additional notes Martin left when he died five years ago.