This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
It’s almost contractually required for Utahns to appreciate the outdoors. My Texan roots have so far prevented me from becoming a skier—hiking is more my speed. Hiking gives me so much: exercise, fresh air, wildlife and interesting rock sightings, and every once in a while, a new perspective on a piece of mathematics. On a recent hike, my spouse and I overestimated our stamina and underestimated the difficulty of the trail we had chosen, and I came to understand Zeno’s paradox on a deeper, more visceral level.
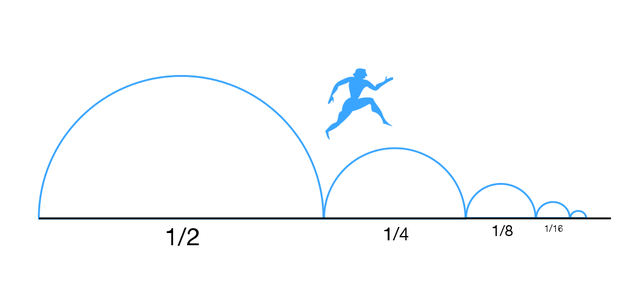
About 2500 years ago, Zeno of Elea posed a few related paradoxes about whether motion was an illusion. The one I pondered on my hike is sometimes called the dichotomy paradox, and it’s probably the one most people think of when Zeno’s paradox comes up in conversation. It goes like this: In order to get from point A to point B, you must first cross half the distance from A to B, then half the remaining distance, then half the remaining distance from that point, and so on. You’ll never arrive at your destination because you have to visit an infinite number of waypoints along your journey.
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
Digging deeper into the argument, even to get to the halfway point, we have yet another Zeno’s paradox to overcome. We must get halfway to the halfway point, and halfway to that point. The reasoning seems to imply that motion is impossible. Yet our lives, and our hikes, are a testament to the fact that we can indeed get from point A to point B.
This paradox is often the first place budding mathematicians wrestle with the concept of infinity and the inherent contradictions we finite beings encounter when we try to make sense of it. But despite its popularity, Zeno’s paradox never really had teeth for me. I was too practical when I first encountered it—obviously I can walk across the room, so why are we even worrying about this? It always seemed a little dopey to me. Until that hike.
The hike was our second tough hike in two days. My calves were tight and achy. Blisters had formed in several places on my feet, growing more tender with each step. My backpack straps and sweaty shirt were chafing my shoulders and hips. Up where we were, above 10,000 feet, every breath felt insufficient, every step was a hard-won victory. And on top of that, I kind of had to pee.
I started checking the GPS on my hiking app obsessively. Each time I checked it, I did a little mental arithmetic. How far was it to the peak? After we turned around, how far did I have left? Before I could get back to the trailhead and the blissful relief of the composting toilet and my car’s comfy seats, I had to make it halfway there. Was that before or after the stream crossing? Once we got to the halfway point, we’d have to cover half the remaining distance back to the trailhead and make it to the treacherously steep switchback section. Once we got there, we still had to reach half the distance to the trailhead. At that point, we saw two moose—a mother and her awkward-looking, but still huge and powerful, offspring—and the paradox seemed all the more real as we stood silently next to the trail, waiting for the animals to eat their fill and move along.
It’s not too hard to interpret and resolve Zeno’s paradox mathematically. Aristotle noted that as the distance decreases, the necessary time does as well. Today we can make his argument more precise, writing down the sum of an infinite series and sometimes even getting a finite number out of it. In the case of Zeno’s paradox, we can represent the situation as the sum of 1/2+1/4+1/8+1/16+…, which adds up to the number 1. Therefore if we move at a constant speed, or even if we get tired but continue to move forward faster than some minimum speed, we will eventually bridge the distance between the two locations.
On the trail, the resolution of Zeno’s paradox isn’t a matter of summing up a slick geometric series. It’s just the audacity to keep putting one foot in front of the other, in spite of the blisters, the chafing, the thin air, and the seductive allure of resting awhile on a comfy rock.
For more information on Zeno’s paradox, check out this recent episode of the BBC’s radio program(me) In Our Time or Vi Hart’s entertaining video about calculus and crosswalks. For another Zeno on a mountain, check out my mathematical big brother Zeno Huang, who also enjoys hiking in the western states.
