This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
Earlier this year, Maryna Viazovska showed how spheres can be most efficiently arranged in eight-dimensional space. It can be baffling to try to think about high-dimensional space, but mathematicians have a few tricks up their sleeves for it. Just as three-dimensional space can be labeled using three coordinates—length, width, and height, or (x,y,z)—eight-dimensional space uses eight coordinates. There’s no limit to the number of dimensions we can study just by adding more coordinates. In any dimension, a sphere is the set of points that are all the same distance from one center point. In two dimensions, the sphere is a circle, and in three it is what we usually think of as a sphere.
Because high-dimensional spaces are difficult, if not impossible, for us to visualize, it’s easy to assume they don’t have any real-world significance. Surprisingly enough, though, they can arise quite naturally.
One way they show up quite naturally is in sewing, which I wrote about earlier this month. In my article about Viazovska’s sphere-packing breakthrough, I mentioned another application of high-dimensional sphere packing: data transmission and error-correcting codes.
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
Here’s the situation: we want to transmit messages over a channel where data might get corrupted in transit. In the real world, think cell phones or fiber-optic cables, or even just trying to have a conversation in a noisy room. The idea is to find a way of communicating that will be robust to small changes in the data that is transmitted.
Take the NATO phonetic alphabet, better recognized by its first three words, alpha-bravo-charlie. If you have to spell your name over the phone, it’s easy for the person on the other end to mistake a B for a P, so it’s helpful to be able to say “B as in bravo.” The words that represent the letters in the phonetic alphabet were chosen so that even with a lot of static, there isn’t any ambiguity about which letter you mean. You’re never saying “B as in bad,” which might leave the other person confused: “D as in dad? P as in pad?”
An error-correcting code is, like the phonetic alphabet, a way to encode data that allows people to reconstruct the message even if the data has been altered in transit. One way to do this is to choose only a finite number of possible messages to transmit and build in some redundancy. For example, if we wanted to transmit only the messages “yes” and “no,” we could decide to encode “yes” as 111 and “no” as 000. If we received the message “101,” we could assume one of the digits had been corrupted in transit but still deduce that the sender had intended to say “yes.” Of course, this code is not perfect. If two digits were corrupted, we would end up misinterpreting the answer, but it is certainly better than nothing.
Sphere-packing comes in when we are trying to find error-correcting codes for sending more complicated messages. In this case, we can think of the data we are transmitting as a point in some high-dimensional space. If we want to transmit messages with 100 pieces of data each, for example, we can see our messages as points in 100-dimensional space. Each coordinate is one of the pieces of data.
Our goal is to find a good set of points in 100-dimensional space that we can use as codewords. What do we want our codewords to do? Well, if some of the pieces of data are changed slightly, we want the codeword to still be identifiable, so we don’t want our codewords to be too similar. In 100-dimensional space, this amounts to each codeword being the center of a 100-dimensional sphere with some small radius. The person sending the message will transmit the coordinates of the center of one of the spheres as their codeword.
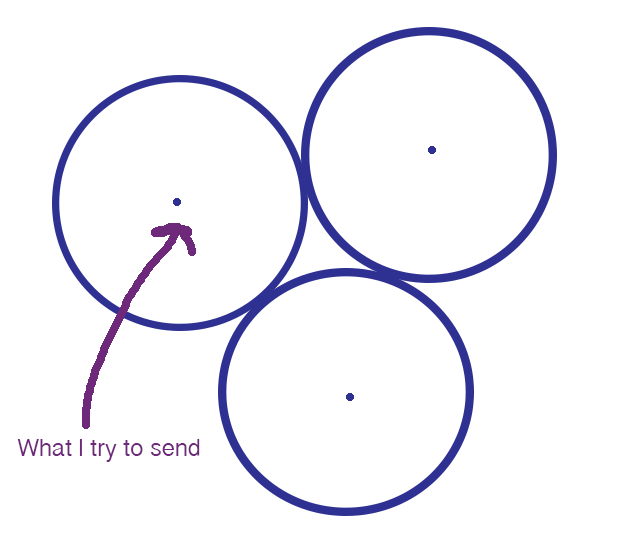
I haven’t gotten the Adobe upgrade where you can draw 100-dimensional spheres, so this 2-dimensional schematic will have to do. Image: Evelyn Lamb
If the coordinates of the point are slightly altered in transit, the receiver will receive a message that isn’t quite the same as what the sender sent.
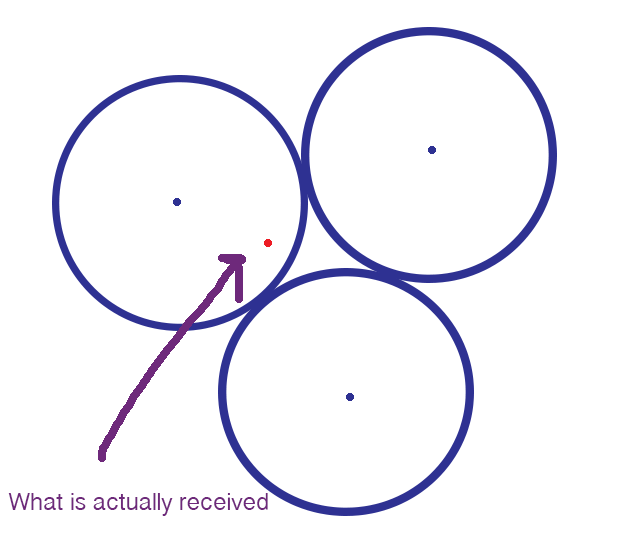
Image: Evelyn Lamb
But if the message is still pretty close to the intended message, the receiver will know what message was intended and correctly interpret the message. Luckily in the diagram above the erroneous message is within a small distance of the message I intended to send, so the recipient will interpret it correctly.
The sphere-packing problem asks how densely we can pack equal-size spheres in, say, 100 dimensions. For error-correcting codes, the centers of these spheres are our codewords. The radius will be chosen based on how much we think our transmission method might jiggle our message around when we send it. If we think the cumulative effect of errors—how much each point can be pushed away in transmission—will be at most 1 unit, we’ll look at packing spheres of radius 1. If it could be 3 units, we pack spheres of radius 3. It doesn’t really matter, though, what the radius is. It’s some number we will choose based on how our transmission technology works.
So we're looking for spheres in 100-dimensional space whose radii are all some set distance away from each other. Surprise! We just found a sphere-packing problem in its natural habitat. Solving the sphere-packing problem in 100 dimensions amounts to figuring out how many codewords we can pack into some defined region in 100-dimensional space. The more efficiently we can pack codewords, the more distinct messages we can send using our 100-dimensional message scheme. That’s why solving the sphere-packing problem can have an important practical effect on data transmission.
One might justifiably ask how important solving the sphere-packing problem is for finding error-correcting codes. We see that the sphere-packing problem is one way to approach an error-correcting code, but perhaps it doesn’t really matter whether we find the very most efficient way to pack them. Is pretty good good enough?
High-dimensional spheres get spiky. That’s a whimsical way to describe two related facts about high-dimensional spheres: the sphere with diameter 1 takes up a smaller and smaller proportion of the volume of the cube with side length 1 as we go up in dimension, and the density of the best sphere packing decreases as dimension increases. In two dimensions, we can fill about 91% of the plane with circles in the beehive-esque optimal hexagonal packing. Efficiently stacked oranges can fill about 74% of three-dimensional space. The sphere-packing problem has not been solved yet in four dimensions, but in eight dimensions, Viazovska showed that the densest packing fills about 25% of space, and in 24 dimensions, the best packing fills only 0.1% of space. In fact, while we don’t know the exact answers for any dimensions other than two, three, eight, and 24, we do know that the upper bound for sphere-packing density decreases exponentially as dimension increases.
The spikiness of the high-dimensional sphere means that even though there is a lot of space in 100 dimensions, we can’t cram codewords in there very well when we’re trying to make an error-correcting code. Hence it is all the more important to find the best sphere packings so we can get as much as possible out of (or into?) a hard-to-fill space.
Viazovska's breakthrough on sphere packing in eight dimensions—and the subsequent solution to the 24-dimensional problem—did not have a practical effect on creating error-correcting codes using those dimensions. Researchers already knew the correct answer to within minute fractions of a percent, so anyone packing spheres in those dimensions was already using the right model. But her work is a proof of concept that a new approach to sphere packing has the potential to make a difference in other dimensions and have a big impact on how we communicate with each other.