This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
The more I learn about continued fractions, the more enamored I am with them. Last week, when I wrote about how much better continued fractions are than the arbitrary decimal digits we usually use to describe numbers, I mentioned that continued fractions tell us the “best approximations” of irrational numbers. Continued fractions are just fractions made of fractions. Every number, rational or irrational, can be written as a continued fraction. In order to get a systematic way to write them, for now we’re going to concentrate on continued fractions that only have ones in the numerators and positive integers in the denominators, although there are some very lovely continued fractions that do not have this property.
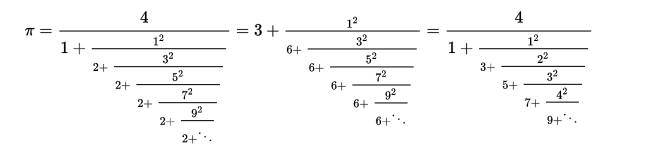
Some beautiful continued fraction representations of pi that don't follow our rules.
We'll be looking at continued fractions that look like this.
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
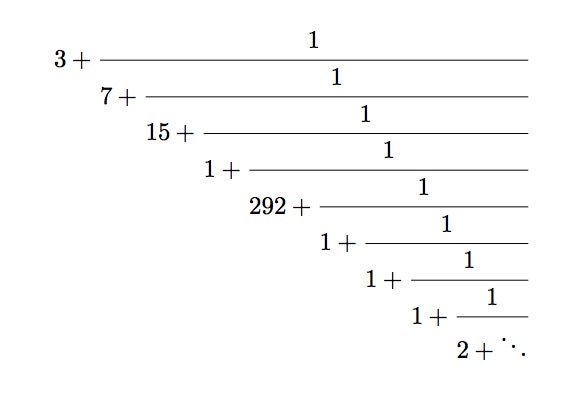
The continued fraction representation of the number pi that does follow our rules.
When we truncate a continued fraction after some number of terms, we get what is called a convergent. The convergents in a continued fraction representation of a number are the best rational approximations of that number. But we need to think about what that means. There's no such thing as a closest rational approximation to an irrational number. By increasing the denominators of our fractions, we can get as close as we want. Truncating a decimal representation of a number is one way to do that. If we want to get a better approximation of the number, we can just add a few more decimal terms. So any reasonable idea of a "best approximation" is relative. It needs to take the size of the denominator into account.
In A. Khinchin’s classic book on continued fractions, he defines two notions of being a "best approximation" to a number. The first is the easier one to describe: a fraction c/d is a best approximation to a number a if c/d is closer to a than any number with a smaller denominator. That is, if |a-c/d|<|a-p/q| for any other fraction p/q where q
All continued fraction convergents are best approximations of the first kind, but they satisfy a property even stronger than that. The basic idea is that if you make the denominator larger, you’re paying a price in some way. It might be in the difficulty of slicing your pizza in to such small pieces (or the cheese you lose slicing it that way), it might be in the computational power required to do calculations with it, it might just be in how much ink and effort it takes to write out the number. But there's a price to be paid. If we’re going to pay this price on the denominator, we want our best approximations to be really good. We don’t just want something that’s marginally better than the last good approximation we got, we want something that’s worth paying a price for the denominator.
The mathematical condition is this: the fraction c/d is a best approximation of the second kind for a number a if for every other fraction p/q with q
Let's look at how it works for pi. John Heidemann at the Information Sciences Institute at USC has a list of all the best rational approximations (of the first kind) of pi with denominators up through about 50 million. The numbers 3/1, 13/4, 16/5, 19/6, and 22/7 are the first few fractions on this list. 13/4 is a little closer to pi than 3 is. It's about 0.1084 away instead of 0.1416. But if we multiply the differences by the denominators, 13/4 doesn't do so well. We get 0.1416×1=0.1416 and 0.1084×4=0.4336, so 13/4 loses pretty badly. The same is true for 16/5 and 19/6. Both of them are a little closer to pi, but they aren't enough closer to make up for their larger denominators. Thus, 13/4, 16/5, and 19/6 are best approximations of the first kind but not of the second kind. But when we get to 22/7, things change. It's quite close to pi. Its difference, 0.00126, is very small. If we multiply it by its denominator, we get 0.00126×7=0.00882. This beats 0.1416 pretty handily, so it's a best approximation of the second kind. It's also the next convergent in the continued fraction for pi.
My favorite convergent in the continued fraction for pi 355/113. It's a really good approximation. It's a continued fraction mic drop. The next best approximation of the first kind has the denominator 16,604. But it isn't even that much better than 355/113. We don't get another decimal digit of accuracy, but we have to increase our denominator by two decimal places. No thanks. We have to increase to the denominator 33,102* before we get a new approximation that's worth bothering with.
That next approximation, 103,993/33,102*, corresponds to the convergent we get when we truncate the continued fraction representation of pi at the 292. This leads to an interesting qualitative observation: the big denominators in the continued fraction for a number tell you that the convergent you got before was a very nice approximation indeed. (For the record, “very nice approximation indeed” is not a technical term.) On the other hand, a small denominator means that the prior convergent wasn't so great. And that makes sense when you think about how fractions work. A big denominator means we just have to add a tiny sliver of something to get closer to our goal.
All continued fraction convergents are best approximations of the second kind, so we can think of them as the best of the best approximations. There are some interesting relationships between the denominators of these approximations and those that are merely the best (i.e. best approximations of the first kind). It gets a bit complicated, but an interesting result is that in order to have best approximations of the first kind that aren't best approximations of the second kind, a continued fraction must have denominators other than one. Therefore, the golden ratio, whose continued fraction is just made up of ones, has only best approximations of the second kind. All of its approximations are the best of the best. On the other hand, with all those ones, its best approximations are the worst that best approximations can be. You could even say that the golden ratio has the worst of the best of the best approximations. Or maybe the best of the best of the worst approximations.
Continued fractions are about excellence. We will not settle for mediocre approximations of numbers (decimals—ugh) or even approximations that are merely the best. Only the best of the best will suffice, only the numbers that are really worth writing down.

Stay thirsty.
*These numbers were corrected after publication—I accidentally overshot on pi convergents!