This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
One of the most frustrating things about studying math is the intuition-obscuring way we write textbooks and academic journal articles. The way we present proofs is not the way we come up with them—it can almost feel like the authors are covering their tracks.
The epsilon-delta proof is a famously unpopular topic among undergraduates in calculus and analysis classes. Delta and epsilon, two small positive numbers, form the scaffold rigorous calculus proofs hang on, and delta-epsilon proofs might be the first place many math students experience the artificiality of the way we present mathematical arguments.
Delta-epsilon proofs relate to a fundamental notion in calculus: that of a limit. Roughly speaking, we say a function tends to a limit L at the point p if the output of the function gets as close as you want to L provided the input is sufficiently close to p. As millions of calculus students have puzzled over for years, we state this rigorously as follows: The function f(x) approaches the limit L as x approaches p if for every ε>0, there exists a δ>0 such that f(x) is within ε of L when x is within δ of p.
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
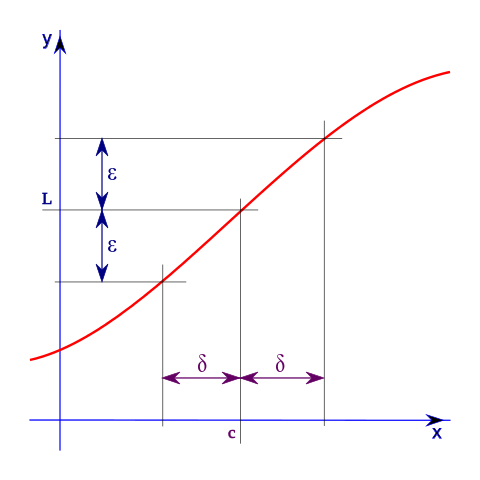
A visual representation of the epsilon-delta definition of limit. When x is within δ of c, f(x)=y is within ε of L. Image: Public domain (by user HiTe) via Wikimedia Commons.
When you write an epsilon-delta proof, especially as an undergraduate, you have to satisfy the letter of the law. You must show that no matter what epsilon you are given, you can figure out the necessary delta. A rigorously written proof starts with the sentence “Let epsilon be greater than 0.” But to discover the proof, you don’t really start with epsilon, you start with delta. You add an arbitrary delta to the input x and see what happens to the output of a function. Then you figure out how to get that output to be less than epsilon.
For example, for the simple function f(x)=2x+1, the internal mental discovery of the proof and the necessary delta will go something like this:
|f(x+δ)-f(x)|=|2(x+δ)+1-(2(x)+1)|=|2(δ)|. So if we want to get f(x+δ) within ε of f(x), we see that 2(δ) needs to be less than or equal to ε. So we conclude that δ=ε/2 will suffice.
When we write the proof, we obscure our thought process:
Let ε>0. Let δ<ε/2. Then |f(x+δ)-f(x)|=|2(x+δ)+1-(2(x)+1)|=|2(δ)|<2(ε/2)=ε. QED. Mic drop.
In the case of this function, it’s not too hard to see where the 2 comes from, and the proof is short enough that any suspense is over quickly anyway. But the change of perspective between delta-first thinking and epsilon-first writing is difficult, even in this simple case.
I vaguely remember writing epsilon-delta proofs for the first time in my high school calculus class. Today, I can look at coefficients and exponents and figure out very quickly what delta will have to be in terms of epsilon, but that first semester, it felt like magic. I never knew at the beginning of my proof discovery process how I would make things work in the end. Although the process was somewhat mysterious, I found it satisfying to figure out what delta had to be and then write out the proof, covering my tracks so I could pull epsilon out of the hat at the end with a flourish.
If Pi Mu Epsilon didn’t already exist, Epsilon Delta would be a perfect name for a math honor society. The epsilon-delta proof is an initiation rite into the secret society of mathematical proof writers.