This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
Last month, I wrote about the hype surrounding a new paper about the much-studied tablet Plimpton 322. This ancient Mesopotamian tablet, which has been the subject of many academic papers over the course of the last few decades, has columns of numbers related to right triangles, but we don’t know exactly how or why the table was created.
In my post, I criticized the publicity video the researchers made to accompany the release of the paper. Specifically, I was irritated at the strange remarks one of the researchers made about the relative utility of base 60, or sexagesimal, versus the base 10, or decimal, system we use today.
To be clear, base 60 has a big advantage over base 10: 60 is divisible by 3, and 10 isn’t. It’s easy to write the fractions 1/2, 1/4, and 1/5 in base 10: they’re 0.5, 0.25, and 0.2, respectively. But 1/3 is 0.3333…. Its decimal representation doesn’t terminate. That really isn’t too much of a problem for us because we are comfortable representing numbers as either decimals or fractions. But the Babylonian number system did not represent fractions in terms of numerators and denominators the way we do. They only used the sexagesimal form, which would be like us only using decimals instead of writing numbers as fractions. In sexagesimal, 1/3 has an easy representation as. It’s 20/60, which could be written as .20 in a sexagesimal system. (It wasn’t written precisely that way by ancient Mesopotamians because they did not have an equivalent to a decimal point. We’ll come back to that later.)
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
The more prime factors, the better when it comes to representing numbers easily using a positional number system like base 10 or 60, but those extra factors come at a cost. In base 10, we only have to learn 10 digits. Base 30, the smallest base that is divisible by 2, 3, and 5 (60 has an extra factor of 2 that doesn’t make a huge difference in how easy it is to represent numbers), requires 30 distinct digits. If we wanted to write fractions like 1/7 using an analogous representation, we’d have to jump all the way up to base 210. Working with so many digits becomes cumbersome very quickly.
Fractions whose denominators only have factors of 2 and 5 have finite decimal representations. Base 12 would be fairly convenient as well. It has prime factors of 2 and 3, and it’s pretty easy to count to 12 on your fingers using the knuckles of one hand instead of the individual fingers. (One of my math history students wrote a post arguing for a base 12, or dozenal, number system.) With base 12, we’d lose the ability to represent 1/5 or 1/10 easily. But 30 or 60, the smallest bases that allow the prime factors 2, 3, and 5, are awfully big. It’s a trade-off. Personally, the idea of having to keep track of 30 or 60 different digits, even if they’re fairly self-explanatory, as the Babylonian digits were, is too much for me, so I’m sticking with 10 or 12. But go ahead and rock the sexagesimal if that's your thing.
Base 60 certainly has that prime advantage over base 10, but I was annoyed by the way Mansfield overstated that advantage in the promotional video they made to accompany the paper. Here’s what I wrote about it last month:
Perhaps the utility of different types of trig tables is a matter of opinion, but the UNSW video also has some outright falsehoods about accuracy in base 60 versus the base 10 system we now use. Around the 1:10 mark, Mansfield says, “We count in base 10, which only has two exact fractions: 1/2, which is 0.5, and 1/5.” My first objection is that any fraction is exact. The number 1/3 is precisely 1/3. Mansfield makes it clear that what he means by 1/3 not being an exact fraction is that it has an infinite (0.333…) rather than a terminating decimal. But what about 1/4? That’s 0.25, which terminates, and yet Mansfield doesn’t consider it an exact fraction. And what about 1/10 or 2/5? Those can be written 0.1 and 0.4, which seem pretty exact.
Indefensibly, when he lauds the many “exact fractions” available in base 60, he doesn’t apply the same standards. In base 60, 1/8 would be written 7/60+30/3600 which is the same idea as writing 0.25, or 2/10+5/100, for 1/4 in base 10. Why is 1/8 exact in base 60 but 1/4 not exact in base 10?
I'm not going to rehash my post here, but I want to clarify one point. A few people who have criticized this criticism of the video think the numbers I mentioned there are just random numbers floating in the ether in the video. They’re not! Because Mansfield did not explain what the numbers meant, they might look random, but in fact, the expression 1/8=7.30 does mean something. I had my students work with base 60 arithmetic a little bit when I taught math history, so I immediately recognized the pairs he displayed as “reciprocal pairs” in base 60. The cuneiform equivalent of the equation 1/8=7.30 would have been meaningful for a mathematically educated person in 1800 BCE.
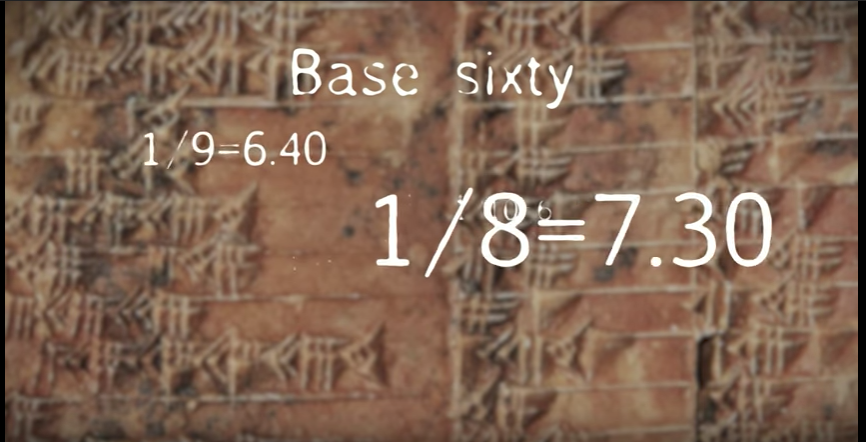
A screenshot from the promotional video researchers made to accompany their paper about the Babylonian tablet Plimpton 322. Credit: UNSW
The Babylonian number system was a positional, or place value, system like ours. In our decimal system, the digit 1 can mean one unit if it’s by itself, ten if it’s in the tens place in a number like 10 or 12, one hundred if it’s in the next place to the left, and so on. In a positional base 60 system, there would be a ones place, a sixties place, a thirty-six hundreds place, and so on, rather than the ones, tens, and hundreds we’re used to. But other than that, the system works the same way ours does. This is in contrast to, for example, Roman numerals, where I means one, X means ten, C means one hundred, and so on. So the Babylonian system is a little easier for us to work with than the Roman system.
But there's a twist: the Babylonian system did not use a zero, at least at the beginning. (I wrote about this quirk when I started teaching math history in 2014.) We use zero as a placeholder, either in the middle of a number, as in the number 101, or at the beginning (0.001) or end (1,000) to indicate the magnitude of the number we’re talking about. Ancient Mesopotamians did not, though they did leave a bit of a space for empty digits in the middle of a number where we would write the zero in 101. They assumed the context would make the order of magnitude clear. In our number system, it would be like writing 1 and assuming it would be clear whether that meant one, ten, one tenth, one hundred, or another number we would write using only the digits one and zero.
That sounds confusing, and it did lead to some errors, but we also make silly errors based on how we write numbers: the digits 6 and 0, or 1 and 7, look similar in some people's handwriting, for example. We even sometimes omit an order of magnitude if it is understood in context. People talk about eating something with 100 calories, which really means 100 kilocalories. Real estate advertisements sometimes say things like “Homes from the $100's” (in Texas suburbs when I was a kid) or “Units from the $500's” (in big cities today). If you show up with a few hundred dollars thinking you’ll come back a homeowner, you’re going to be very sorry you didn’t understand the tacit “thousand” at the end of those numbers.
Today, computers generally represent and manipulate numbers using floating-point arithmetic, which might remind you of scientific notation. One set of digits indicates the digits in the number and the other set indicates its order of magnitude. That way it takes basically the same amount of memory to store the number 12 as the number 12,000,000. Although the Babylonian system did not indicate orders of magnitude as clearly as modern computers, the similarities are enough for some people to refer to it as sexagesimal floating-point.
The fact that 1 could indicate one, sixty, thirty-six hundred, or other powers of 60 in the Babylonian number system led to a different way of thinking about division. If they had to divide by a number they would multiply by a “reciprocal” of that number. Two numbers would be reciprocals if their product was the digit 1. But that could mean anything that was written as the equivalent of the digit 1 in base 60: 1, 60, 3600, 1/60, and so on. So 4 and 15 form a reciprocal pair in base 60 because 4×15 is 60. So do 3 and 20, 5 and 12, and many other combinations. (These pairs might feel familiar: there are 15 minutes in a quarter of an hour, 20 in a third, and so on. I like to think of this as vestigial sexagesimism.) Reciprocal tables included more complicated reciprocal pairs as well: 8 and 7,30; 9 and 6,40; 1,21 and 44,26,40. (Today, we typically put commas between sexagesimal digits when we write them with our Hindu-Arabic decimals to avoid ambiguity. 7,30 means one place has a 7 in it and one has a 30. The order of magnitude still depends on context.)
At first, statements like 1/4=15 and 1/8=7,30 felt unnatural to me and my students, but I think translating them back to base 10 can help a bit. When I was a kid, I discovered an amazing fact: instead of multiplying by 5, which was difficult for me, I could divide by 2, which was easy for me, and multiply by 10. I didn’t think of it quite that way. I thought of it more as “divide by 2 and then make the number the right size.” Later I discovered that one could reverse the process: you can divide by 5 by multiplying by 2 and making the number the right size (by dividing by 10, which can look like taking away a zero or moving a decimal point to the left)! I also found that I could multiply by 50 by using the same trick and adding another 0.
I was quite pleased with these little tricks but never told my teachers because I was certain I was cheating. If caught, I would have to learn how to multiply or divide by 5. The horror! I know now why my tricks worked and that they weren’t cheating. I was using the fact that 5 and 2 are decimal floating-point reciprocals. In fact, it’s good to be able to break numbers apart in convenient ways to make arithmetic easier. When I first encountered the Babylonian base 60 system, I recognized the 5-2 trick as a base 10 version of sexagesimal “reciprocal pairs.” While Mesopotamian mathematics probably isn't going to change the way we do trigonometry, playing with numbers and learning about different ways of representing them can help students (and non-students) develop our number sense and have fun.
For more on the Babylonian number system: An introduction to Babylonian numerals from the MacTutor math history website Duncan J. Melville's Mesopotamian Mathematics page; see in particular "Special Topics," which includes articles about Babylonian reciprocal pairs