This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
Note: Coincidentally, this post was published shortly after news came out about Facebook's disturbing, possibly illegal practice of allowing businesses to exclude users from seeing certain ads based on "ethnic affinity." I'd love for you to read my silly blog post about using Facebook to have fun with Ramsey theory, but if you're only going to read one article related to Facebook today, Pro Publica's piece exposing this alarming practice is definitely more important.
Almost every morning, I check Facebook to see which of my friends are celebrating their birthdays. I rarely wish them a happy birthday because it seems so impersonal to do that online. (Ironically, it always makes me feel great to get birthday wishes on Facebook from so many friends, even ones I don’t talk with often. Do I contradict myself? Very well, then I contradict myself. I am large, I contain multitudes.) But I like to start my morning with a little Ramsey theory: I get excited if all the friends who share a birthday know each other or if none of them know each other.
Ramsey theory is enigmatically defined on Wikipedia as “a branch of mathematics that studies the conditions under which order must appear.” That’s rather poetic, and I think if you already know what Ramsey theory is, it seems like a good definition. But perhaps an example will make it more clear what “conditions under which order must appear” means.
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
The go-to example for Ramsey theory is often called the theorem on friends and strangers, and it’s where I get my Facebook birthday check inspiration: if there are at least six people at a party, there must be a group of three people who all know each other or three people who are all strangers. Mathematician Simon Pampena explains it for Numberphile if you want more details on why that’s true. If you have a party with only five people at it, on the other hand, you don’t have a guarantee. This blue star inside a red pentagon is proof.
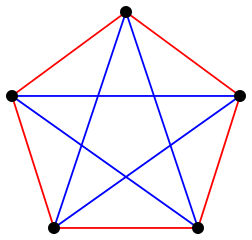
Imagine that the vertices of the pentagon are the five people at the party, and there’s a blue line between them if they know each other and a red line between them if they’re strangers. We can see that every triangle has either two red edges and one blue or two blue edges and one red.
Credit: Richtom80 Wikimedia (CC BY-SA 3.0)
What does the theorem on friends and strangers have to do with order that must appear? The order here is the three people who are all friends or strangers, and the “must appear” is the fact that having six people at the party makes that triangle of friends or strangers mandatory.
People who study Ramsey theory would say that the Ramsey number R(3,3)=6. The Ramsey number R(m,n) is the smallest number of people you’d have to invite to a party to be guaranteed that m people all know each other or n people are all strangers. (The numbers m and n don’t have to be the same.) If you wanted to be sure you could find 3 mutual friends or 4 mutual strangers, you’d be asking for the Ramsey number R(3,4), which happens to be 9.
My morning Facebook ritual got me wondering whether there are any interesting Ramsey theory questions I can ask about my Facebook friends. The birthday thing throws an extra layer of structure into the normal Ramsey number problem. Now instead of looking at all my friends as one big group, I’ve split them up into 366 smaller groups, one for each possible birthday. (Yes, I have friends born on Leap Day.) The question I’m curious about is whether it’s necessary for any of the nodes that are the same color to be a group of mutual friends or mutual strangers. I know that it’s true for my personal group of friends, but would it have to be true for anyone with the same number of friends I have? Or to be a little more specific, I know I have days of the year with six friends who are mutual friends or mutual strangers. Is that necessary for anyone who has the same number of Facebook friends I do? What is the minimum number of Facebook friends for which this has to be true?
When I thought about this for a while, I realized the birthday grouping is a red herring. Any day of the year could have between 0 and all of my friends’ birthdays on it. For some questions I have, you have to look at the edge case in which the birthdays are all the same day, and for some you have to look at the edge case where they’re maximally spread out. Either way, you don’t get questions that are much more or less interesting or difficult than the questions without dividing people up by birthday. Oh well, you win some, you lose some.
What’s the point? It’s not just to throw a few Ramsey theory factoids at you, although I do enjoy those factoids. I just wanted to share a little way in which a little bit of math enhances my life a little. So much talk about math, particularly math education, centers on why math is useful for jobs or everyday life. We also see a fair amount of mysticism about mathematical beauty. Those are both fine, but I also just enjoy having math as another lens with which to see the world. The fact that I know a little bit about Ramsey theory means that most mornings (there are some days none of my Facebook friends have a birthday), I think about a few of my friends on their birthdays for a few extra seconds while I check to see if there’s an interesting configuration of friends or strangers in there. So far the largest interesting group I’ve noticed is six mutual strangers I know born on March 5th. I’m crossing my fingers that one of these days I hit seven!