Lambert on Love and Hate in Geometry

This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American

The history of hyperbolic geometry is filled with hyperbolic quotes, and I came across a beautiful one earlier this semester in my math history class. Johann Heinrich Lambert, a Swiss mathematician who lived from 1728-1777, was trying to prove the parallel postulate and thereby establish beyond a shadow of a doubt the truth of Euclidean geometry but ended up proving some very curious things about non-Euclidean geometry instead.

Lambert's investigations into geometry involved a figure now known as the Lambert quadrilateral. (It is somewhat inaptly named because the 10th-11th century Arab mathematician Ibn al-Haytham used them more than 700 years before Lambert did.) The Lambert quadrilateral has four sides and three right angles.

On supporting science journalism

If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.

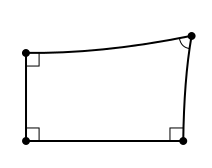
A Lambert quadrilateral that appears to have an acute angle as the fourth angle. Image: public domain, via Wikimedia Commons.

In high school geometry, the angles in a quadrilateral must sum up to 360°, but this fact is based on assuming the Euclidean parallel postulate. In a Euclidean Lambert quadrilateral, the fourth angle must also be 90°. Lambert wanted to show that the fourth angle had to be 90° without using the parallel postulate. To do this, he explored three possibilities corresponding to the the angle measure of the fourth angle: the hypothesis of the right angle, the hypothesis of the obtuse angle, and the hypothesis of the acute angle. Today, we would say that these three hypotheses correspond to Euclidean, elliptic or spherical, and hyperbolic geometry. Lambert discovered that under the third hypothesis, some perplexing things happen: the area of a triangle depends on its angle sum, and there is an "absolute" measure of length, that is, a triangle can't be made larger without distorting its angles. These results troubled Lambert, and he wrote*:

"It is easy to see that under the third hypothesis one can go even further and that analogous, but diametrically opposite, consequences can also be found under the second hypothesis. But, for the most part, I looked for such consequences under the third hypothesis in order to see if contradictions might not come to light. From all this it is clear that it is no easy matter to refute this hypothesis. I will cite some more consequences without considering to what extent they can be extended, mutatis mutandis, under the second hypothesis.

"The most striking of these consequences is that under the third hypothesis we would have an absolute measure of length of every line, of area of every surface and of volume for every physical space. This refutes an assertion that some unwisely hold to be an axiom of geometry, for until now no one has doubted that there is no absolute measure whatsoever. There is something exquisite about this consequence, something that makes one wish that the third hypothesis be true!

 

"In spite of this gain I would not want it to be so, for this would result in countless inconveniences. Trigonometric tables would be infinitely large, similarity and proportionality of figures would be entirely absent, no figure could be imagined in any but its absolute magnitude, astronomers would have a hard time, and so on.

 

"But all these are arguments dictated by love and hate, which must have no place either in geometry or in science as a whole."

Admirably, Lambert recognized that his distaste for the implications of the third hypothesis didn't make it invalid. But it is interesting that Lambert found the idea of an absolute length measure so distasteful—it's sitting right under our noses. On a sphere, there is only one size of triangle with any given set of angles. If you want to make a triangle that's larger but has the same angles, you have to draw it on a larger sphere. Once you fix the size of a sphere, you fix the size of all triangles.

Today, thanks to the labors of Bernhard Riemann and many others, we have a very different conception of geometry than Lambert did. Lambert was trying to prove that Euclidean geometry was the true geometry. Now, we have an axiomatic view: Euclidean geometry is the true geometry that results from the axioms of Euclid, but if we change those axioms, we get different results that are valid in different contexts. Spherical geometry starts from a different set of axioms. Modern mathematicians don't think that spherical geometry is right and Euclidean geometry is wrong, or vice versa. They're just different axiomatic systems. Lambert came tantalizingly close to that viewpoint when he compared the third hypothesis to the second, but he didn't quite get there. He wrote:

"To come back to the third hypothesis [that of the acute angle]. As we have just seen, under this hypothesis the sum of the three angles in every triangle is less than 180 degrees, or two right angles. But the difference up to 180 degrees increases like the area of the triangle; this can be expressed thus: if one of two triangles has an area greater than the other then the first has an angle sum smaller than the second....

"I will add just the following remark. Entirely analogous theorems hold under the second hypothesis [that of the obtuse angle] except that under it the angle sum in every triangle is greater than 180 degrees. The excess is always proportional to the area of the triangle.

"I think it remarkable that the second hypothesis holds if instead of a plane triangle we take a spherical one, for its angle sum is greater than 180 degrees and the excess is also proportional to the area of the triangle.

 

"What strikes me as even more remarkable is that what I have said here about spherical triangles can be proved independently of the difficulty posed by parallel lines and upon assuming solely the axiom that every plane through the center of a sphere divides it into two equal parts.

 

"From this I should almost conclude that the third hypothesis holds on some imaginary sphere. At least there must be something that accounts for the fact that, unlike the second hypothesis, it has for so long resisted refutation on planes."

Although hyperbolic geometry doesn't hold on an "imaginary sphere" (assuming he meant a sphere with an imaginary number as a radius), Lambert's observation is keen. The formula for the area of a triangle on a sphere is K²(a+b+c-180), where a, b, and c are the measures of the three angles of the triangle and K is a constant that depends on the radius of the sphere. The formula for the area of a triangle in hyperbolic geometry is K²(180-a-b-c). If we imagine (har!) that the K in the first formula is an imaginary number, then its square is negative, and we get the second formula. (For the curious, in both cases, K is the curvature of the surface containing the triangle. Curvature is one of the key building blocks in our modern treatment of geometry.)

Lambert was close to making the breakthrough that would bring a new era of geometry, but the honor ended up going to János Bolyai and Nikolai Lobachevsky over 50 years after Lambert's death. Still, his words about love, hate, and imaginary spheres demonstrate the passion and creativity (tempered by a dose of level-headed logic) that have always been essential in mathematics and eventually led to the non-Euclidean revolution.

* All excerpts from Lambert come from the English translation of A History of Non-Euclidean Geometry by B.A. Rosenfeld. Bold emphasis is mine.