This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
Today on My Favorite Theorem, my cohost Kevin Knudson talks with Justin Curry, a mathematician at the University at Albany in the SUNY system. They recorded live at a topological data analysis conference at the Banff International Research Station in Canada. You can listen here or at kpknudson.com.
Dr. Curry’s favorite theorem is the classification of the Platonic solids. These are the five convex polyhedra—tetrahedron, cube, octahedron, dodecahedron, and icosahedron—that are made of congruent regular polygons. The tetrahedron, octahedron, and icosahedron are made of four, eight, and twenty, respectively, equilateral triangles, the cube of six squares, and the dodecahedron of twelve regular pentagons. The fact that there are no other polyhedra that are quite as regular is a long-known but still beautiful and striking theorem.
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
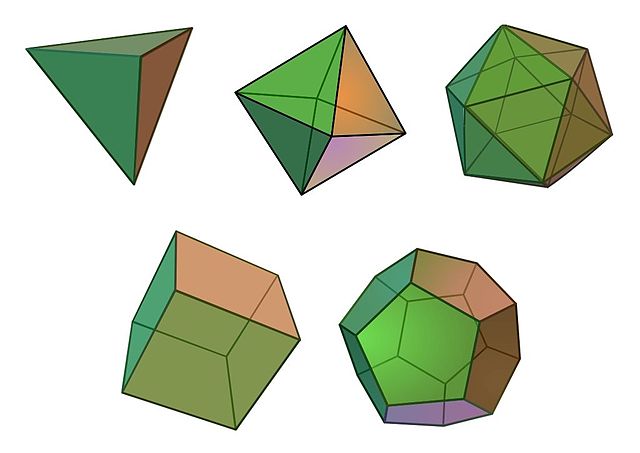
The Platonic solids. Top row: tetrahedron, octahedron, icosahedron. Bottom row: cube, dodecahedron. Credit: Максим Пе Wikimedia(CC BY-SA 4.0)
They also talked about the idea of duality in geometry. For any polyhedron, you can replace vertices with faces and faces with vertices to get a new polyhedron. When you do this to a Platonic solid, you get another Platonic solid as a dual. The cube is dual to the octahedron, the dodecahedron to the icosahedron, and the tetrahedron to itself. Dr. Curry likes these solids and their duality so much that he got tattoos of them. He has tetrahedra from Johannes Kepler, a cube-octahedron duality design from the artist alucinori, and a dodecahedron-icosahedron duality tattoo of his own design. If you aren’t quite ready for that level of commitment, Kevin suggests you might enjoy making the solids out of origami instead using Thomas Hull’s book Project Origami: Activities for Exploring Mathematics.
In each episode of the podcast, we ask our guest to pair their theorem with something: food, beverage, music, literature, or any other delight in life. For his pairing, Dr. Curry went literal—literally. He pairs the Platonic solids with Plato’s Timaeus, where Plato puts forth some of his ideas about the nature of the universe. He associates four of the Platonic solids—tetrahedron, cube, octahedron, and icosahedron—with the four elements: fire, earth, air, and water. The dodecahedron is supposed to be the shape of the universe as a whole. You’ll have to listen to the episode to hear Dr. Curry’s thoughts about how the idea of duality in the solids is reflected in those associations.
The Platonic solids were important to Johannes Kepler’s cosmology as well. His 1596 treatise Mysterium Cosmographicum contains his theory of the universe as a nesting set of Platonic solids. It didn’t quite end up working out that way, but it sure looks cool.
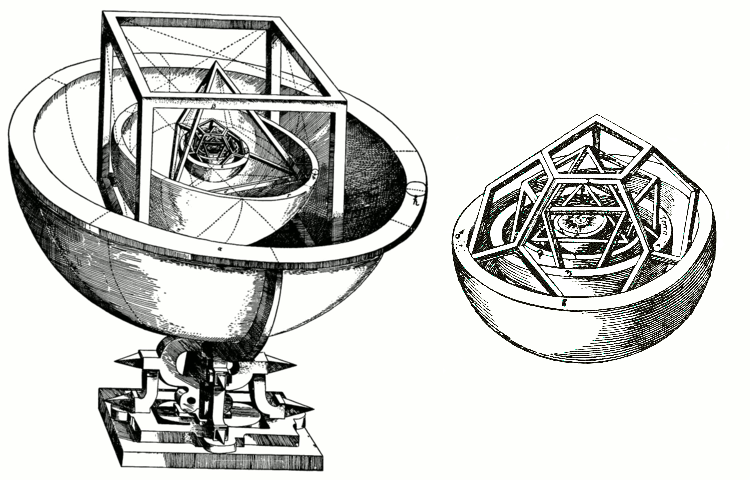
Kepler's model of the solar system based on Platonic solids, with a detail of the inner planets on the right. Credit: Mysterium Cosmographicum Wikimedia
You can find more information about the mathematicians and theorems featured in this podcast, along with other delightful mathematical treats, at kpknudson.com and here at Roots of Unity. A transcript is available here. You can subscribe and review the podcast on iTunes and other podcast delivery systems. We love to hear from our listeners, so please drop us a line at myfavoritetheorem@gmail.com. Kevin Knudson’s handle on Twitter is @niveknosdunk, and mine is @evelynjlamb. The show itself also has a Twitter feed: @myfavethm and a Facebook page. Join us next time to learn another fascinating piece of mathematics.
Previously on My Favorite Theorem:
Episode 0: Your hosts' favorite theorems Episode 1: Amie Wilkinson’s favorite theorem Episode 2: Dave Richeson's favorite theorem Episode 3: Emille Davie Lawrence's favorite theorem Episode 4: Jordan Ellenberg's favorite theorem Episode 5: Dusa McDuff's favorite theorem Episode 6: Eriko Hironaka's favorite theorem Episode 7: Henry Fowler's favorite theorem
