This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
The other day I ran across a sentence on one of my favorite blogs, Math Professor Quotes, that kind of blew my mind: “The log log of any number in the universe is effectively less than five.”
In case your high school math days are a bit foggy, the log (short for logarithm) of a number is basically its order of magnitude. It’s not clear whether the anonymous math professor is talking about the log base 10 or the natural log or some other log he or she prefers, but it doesn’t really matter. The idea is the same.
More technically, if y=log(x) and we’re talking log base 10, it means y is the number that makes 10y equal to x. So log(10)=1 and log(100)=2 because 10^1=10 and 10^2=100.* The logarithm is the inverse of an exponential function. I think of it as a "flattening" function: all numbers between 10 and 100 have a log between 1 and 2, and all numbers between 100 and 1000 have a log between 2 and 3. The differences are flattened out.
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
The log log of a number, then, is the order of magnitude of the order of magnitude. It flattens numbers even more. Just as exponents grow faster than multiplication (and up-arrows grow faster than exponents), log grows more slowly than multiplication and log log grows more slowly than log. Whereas log 10 and log 100 differed by 1, their log logs differ by only 0.3. It isn't until 10,000,000,000 that log log even gets to 1.
So is the log log of any number in the universe less than five? Now it may matter which base the professor meant. If the professor meant log base 10, then any number less than 10^10^5, a 1 followed by 100,000 zeroes, has a log log of less than 5. I don't know about you, but I don't have much call for numbers that big in my everyday life.
However, I’m guessing the good professor probably meant the natural logarithm, or log base e, because that's the one mathematicians typically go for. I'm going do write this as "ln" to avoid ambiguity, though I'll note that in my head, I'm still pronouncing it "log."
Even with the base e, numbers with a ln ln of 5 are impossibly huge. The number e^e^5 is about 3x10^64, so the ln ln of any number less than that is less than 5. I rarely think even fleetingly about numbers this big. For reference, there are about 1080 atoms in the universe. If we regularly talked about all the atoms at once, we would have call for a number whose ln ln is 5.2. Rounding up to a googol doesn’t change it much: now we’re at about 5.4.
Contemplating how slowly log log grows and how much it flattens out the number line, I got to thinking about some infinite series I first met in second semester calculus that still fascinate me. First, the harmonic series:
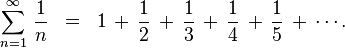
The harmonic series diverges, meaning even though the terms get smaller and smaller, the sum is infinite. (I won’t take away the fun of figuring out why it’s infinite, but I will give you a hint: think about grouping terms and see if you can get all the groups to be bigger than 1/2.)
Although the harmonic series diverges, it diverges pretty slowly. Ben Orlin reports that the total after one googol terms is about 230. In other words, counting up by tiny fractions is an inefficient way to get to infinity.
What does that have to do with log logs? Well, there is a divergent series that escapes to infinity even more slowly than the harmonic series: the sum from 2 to infinity of 1/n(ln(n)). (Why 2 to infinity instead of 1? If we tried to include an n=1 term, we'd be consumed by the conflagration that results from dividing by ln(1), also known as 0.)
Let’s think about what’s happening with the series ∑1/n(ln(n)). Every term is smaller than the corresponding term of the harmonic series, which diverges. On the other hand, it's larger than the corresponding term of 1/n2, which converges.
Fortunately, we can pull in some integrals to convince ourselves that ∑1/n(ln(n)) does indeed diverge. The function 1/x is kind of like the sequence 1/n. The function just interpolates between the steps of the sequence.

A plot of the function y=1/x and steps that each have height 1/n for n=1, 2, 3, and so on. The area under the curve of the function 1/x is shaded darkly, and the area under the steps is shaded lightly. Image created with Desmos.
The integral of the function y=1/x (the area under the curve above) is connected to the sum of the series ∑1/n: either both are finite, or both are infinite. This gives us a not quite as fun way to prove the harmonic series diverges: the integral of 1/x is ln(x), which grows arbitrarily large, so the area under the curve from x=1 all the way out to infinity is infinite.
In general, comparing infinite series to integrals of continuous functions is a good way to get a handle on whether the sums are finite or infinite. For the series ∑1/n(ln(n)), we compare it to the function y=1/x(ln(x)). If we can figure out whether the integral of 1/x(ln(x)) is finite, we’ll know whether the series converges.
The details aren’t important here, but it turns out that the integral of 1/x(ln(x)) is ln(ln(x)), our beloved log log. Once again, there is no bound to what log log of a number can be, so both the integral from 2 to infinity of 1/x(ln(x)) and the sum from 2 to infinity of 1/n(ln(n)) are infinite.
If you thought the harmonic series diverged slowly, you will be blown away by ∑1/n(ln(n)). The sum of the harmonic series was 230 after a googol terms. The sum of the first googol terms of 1/n(ln(n)) is around ln(ln(one googol)), which you may recall was 5.4. If you want to get all the way up to 230 taking steps of size 1/n(ln(n)), you'll be walking for a pretty long time.
But wait, there’s more! (Or less, depending on how you look at it.) The majestic chain rule allows us to build a whole family of series that all go to infinity, each more slowly than the last. We just start stacking logs.

Image: Aapo Haapanen, via Flickr.
It gets silly fast. The sum of ∑1/n(ln(n))(ln(ln(n))) is kind of like the integral of 1/x(ln(x))(ln(ln(x))). That integral is ln(ln(ln(x))), so the sum of ∑1/n(ln(n))(ln(ln(n)) up to a googol is about 1.69.
The series ∑1/n(ln(n))(ln(ln(n)))(ln(ln(ln(n)))) grows even more slowly. The function we compare that to, 1/x(ln(x))(ln(ln(x)))(ln(ln(ln(x)))), has an integral of ln(ln(ln(ln(x)))). At a googol, that value is just over a half.
We can keep adding logs all day and get series that diverge more and more slowly. The one weirdness I'm sweeping under the rug is finding the right place to start each series or integral. You don't want to divide by 0 accidentally or try to take the natural log of a negative number, so you'll have to start each series a bit later than the last to avoid these complications.
I can't think of a practical reason I'd want to find ∑1/n(ln(n))(ln(ln(n)))(ln(ln(ln(n)))) starting at n=16, but I think it's fun to contemplate these agonizingly slow trips to infinity and beyond. After all, life is about the journey, not the destination.
*If you are viewing this post on the new version of the Scientific American website, the exponents may not be formatted correctly. There may be an option at the top of the page to view it on the old version of the website instead.
